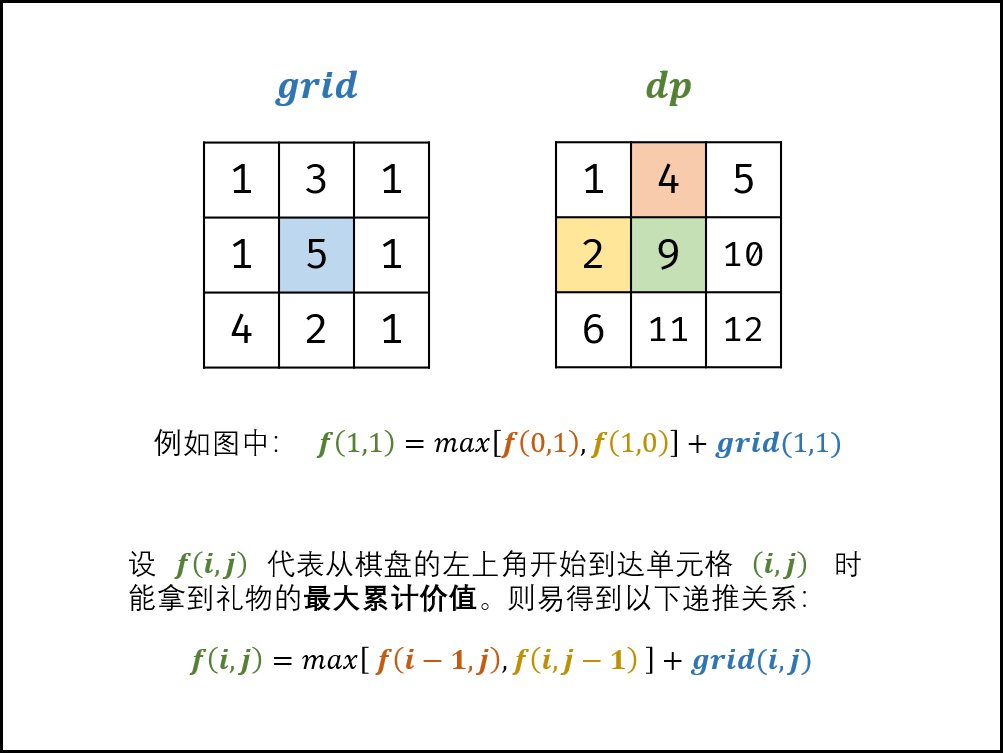剑指 Offer 刷题笔记

LeetCode 剑指 Offer 刷题笔记

✔️Day 1

刷题笔记：《剑指 Offer 第一天》

09.用两个栈实现队列

题目：剑指 Offer 09. 用两个栈实现队列

剑指 Offer 09

解题思路

用两个栈来管理进队出队，stack1 负责进队，stack2 负责出队；

  • stack2 不为空时直接从 stack2 出栈即可

  • 当 stack2 为空时将 stack1 中的所有元素放入 stack2 中，此时栈中的元素已经完成了 reverse 反转，可以正常出栈即为 出队

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class CQueue {
  private Stack<Integer> stack1;
  private Stack<Integer> stack2;
  public CQueue() {
    stack1 = new Stack();
    stack2 = new Stack();
  }
  public void appendTail(int value) {
    stack1.push(value);
  }
  public int deleteHead() {
    if (stack2.isEmpty()) {
      while(!stack1.isEmpty()) {
        stack2.push(stack1.pop());
      }
      if (stack2.isEmpty()) {
        return -1;
      }
    }
    return stack2.pop();
  }
}

30.包含 main 函数的栈

题目：剑指 Offer 30. 包含min函数的栈

剑指 Offer 30

题解代码

看了题解发现了好多种思路，大体上有两种：

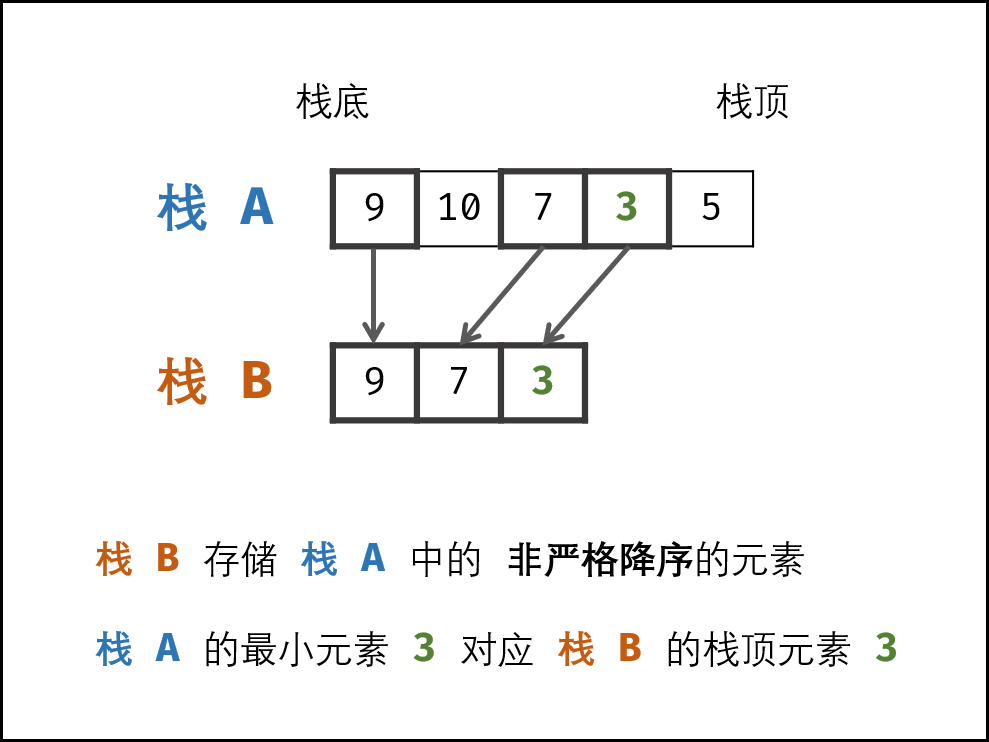
  1. 空间换时间，每次压栈都会将栈顶元素与当前元素比较，并将这个值记录下来，等于说栈内每个元素都是一个数p组， stack.push([压栈元素，当前栈最小值])
    官方题解优化了一点，构造了一个 降序辅助栈 ，内存消耗更少了些。
    LeetCode Krahets 图解

  2. 第二种思路巧妙，利用差值法将存入元素进行变换，出栈时再进行还原；

    • 每次存入：原来值 - 当前最小值
  • 存入的是：非负数 -> 栈中的值 + 当前最小值 (还原)
    • 存入的是：负数 -> 当前最小值 - 栈顶 (还原)， 且更新最小值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class MinStack {
  Stack<Long> A;
  long m;
  public MinStack() {
    A = new Stack<Long>();
  }
  public void push(int x) {
    if (A.isEmpty()) {
      A.push((long) 0);
      m = (long) x;
    } else {
      A.push((long) x - m);
      m = Math.min((long) x, m);
    }
  }
  public void pop() {
    long p = A.pop();
    if (p < 0) {
      m = m - p;
    }
  }
  public int top() {
    long p = A.peek();
    if (p < 0) {
      return (int) m;
    } else {
      return (int) (m + p);
    }
  }
  public int min() {
    return (int) m;
  }
}

二刷代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class MinStack {
  private Stack<Integer> stack1;
  private Stack<Integer> stack2;
  /** initialize your data structure here. */
  public MinStack() {
    stack1 = new Stack();
    stack2 = new Stack();
  }
  public void push(int x) {
    stack1.push(x);
    if (stack2.isEmpty()) {
      stack2.push(x);
      return;
    }
    if (x <= stack2.peek()) {
      stack2.push(x);
    }
  }
  public void pop() {
 // 这里有个坑，对象之间的比较不能用 == 返回的是 Integer，相同对象之间不会装箱拆箱
    if (stack2.peek().equals(stack1.pop())) {
      stack2.pop();
    }
  }
  public int top() {
    return stack1.peek();
  }
  public int min() {
    return stack2.peek();
  }
}

✔️Day 2

刷题笔记：《剑指 Offer 第二天》

06. 从尾到头打印链表

题目：剑指 Offer 06. 从尾到头打印链表

剑指 Offer 06

解题思路（两种）

  1. 由于链表的不确定性（长度不确定），我使用了栈去存储链表的每个结点的值最后一一出栈，存入数组中得到答案。
  2. 二次遍历链表，第一次遍历获取链表的长度 len，第二次遍历将链表的值反向压入数组中 [len - 1 - i]。

两种方案思路基本一致，方案二时间上应该是与第一种方案无异，在空间上节省了一个存储栈（辅助栈）的空间。

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
  private final Stack<Integer> stack = new Stack<>();
  public int[] reversePrint(ListNode head) {
    while(head != null) {
      stack.push(head.val);
      head = head.next; 
    }
    int[] retVal = new int[stack.size()];
    int count = 0;
    while(!stack.isEmpty()) {
      retVal[count++] = stack.pop();
    }
    return retVal;
  }
}

二次解答（递归）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Solution {
  private int[] retVal;
  private int i = 0;
  private int j = 0;
  public int[] reversePrint(ListNode head) {
    solve(head);
    return retVal;
  }
  public void solve(ListNode head) {
    if (head == null) { // 终止条件
      retVal = new int[i]; // 确定链表长度
      return;
    }
    ++i;
    solve(head.next);
    retVal[j++] = head.val;
  }
}

24. 反转链表

题目：剑指 Offer 24. 反转链表

剑指 Offer 24

解题思路

  1. 和剑指 Offer 6 一样使用辅助栈即可。

  2. 看了题解，使用双指针实现；

解题思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
  private final Stack<ListNode> stack = new Stack<>();
  public ListNode reverseList(ListNode head) {
    if(null == head) { // 特例：空链表
      return head;
    }
    while(head != null) {
      stack.push(head);
      head = head.next;
    }
    ListNode revHead = stack.pop();
    ListNode node = revHead; 
    while(!stack.isEmpty()) {
      node.next = stack.pop();
      node = node.next;
    }
    // 将最后一个节点的 next 节点置空(它本来指向反转后的上一个节点)
    node.next = null;
    return revHead;
  }
}

二刷（双指针）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private final Stack<ListNode> stack = new Stack<>();
public ListNode reverseList(ListNode head) {
  if(null == head) { // 特例：空链表
    return null;
  }
  ListNode revHead = null,tmp = null;
  while (head != null) {
    tmp = head.next;
    head.next = revHead;
    revHead = head;
    head = tmp;
  }
  return revHead;
}

画图演示清楚即可，附上 leetcode 动态演示图；

LeetCode krahets 图解

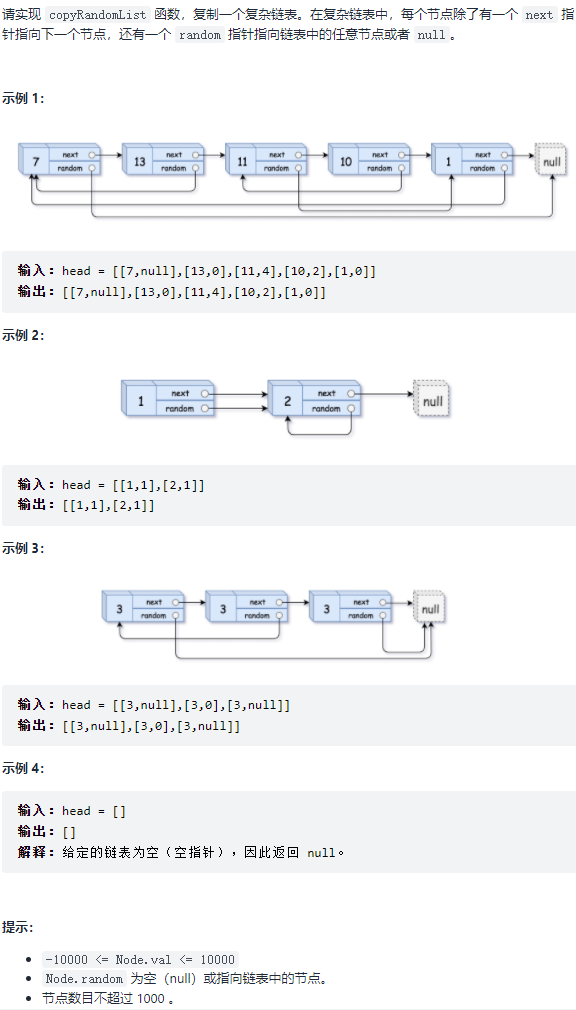
35. 复杂链表的复制

题目：剑指 Offer 35. 复杂链表的复制

剑指 Offer 35

思路一

利用哈希表的查询特点，考虑构建 原链表节点 和 新链表对应节点 的键值对映射关系，再遍历构建新链表各节点的 next 和 random 引用指向即可。

算法流程

  1. 若头节点 head 为空节点，直接返回 null；
  2. 初始化： 哈希表 dic ， 节点 cur 指向头节点；
  3. 复制链表：
    1. 建立新节点，并向 dic 添加键值对 (原 cur 节点, 新 cur 节点） ；
    2. cur 遍历至原链表下一节点；
  4. 构建新链表的引用指向：
    1. 构建新节点的 next 和 random 引用指向；
    2. cur 遍历至原链表下一节点；
  5. 返回值： 新链表的头节点 dic[cur] ；

复杂度分析

  • 时间复杂度 O(N)： 两轮遍历链表，使用 O(N) 时间。
  • 空间复杂度 O(N) ： 哈希表 dic 使用线性大小的额外空间。

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Solution {
  public Node copyRandomList(Node head) {
    if(head == null) return null;
    Node cur = head;
    Map<Node, Node> map = new HashMap<>();
    // 3. 复制各节点，并建立 “原节点 -> 新节点” 的 Map 映射
    while(cur != null) {
      map.put(cur, new Node(cur.val));
      cur = cur.next;
    }
    cur = head;
    // 4. 构建新链表的 next 和 random 指向
    while(cur != null) {
      map.get(cur).next = map.get(cur.next);
      map.get(cur).random = map.get(cur.random);
      cur = cur.next;
    }
    // 5. 返回新链表的头节点
    return map.get(head);
  }
}

思路二

考虑构建 原节点 1 -> 新节点 1 -> 原节点 2 -> 新节点 2 -> …… 的拼接链表，如此便可在访问原节点的 random 指向节点的同时找到新对应新节点的 random 指向节点。

算法流程

  1. 复制各节点，构建拼接链表:
    • 设原链表为，构建的拼接链表如下所示：
  2. 构建新链表各节点的 random 指向：
    • 当访问原节点 cur 的随机指向节点 cur.random 时，对应新节点 cur.next 的随机指向节点为 cur.random.next 。
  3. 拆分原 / 新链表：
    • 设置 pre / cur 分别指向原 / 新链表头节点，遍历执行 pre.next = pre.next.next 和 cur.next = cur.next.next 将两链表拆分开。
      返回新链表的头节点 res 即可。

复杂度分析

  • 时间复杂度 O(N)： 三轮遍历链表，使用 O(N) 时间。
  • 空间复杂度 O(1)： 节点引用变量使用常数大小的额外空间。

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class Solution2 {
  public Node copyRandomList(Node head) {
    if (head == null) return head;
    Node cur = head;
    while (cur != null) { // 构造新的节点 node1 -> new node1 -> node2 -> new node2
      Node newNode = new Node(cur.val);
      newNode.next = cur.next;
      cur.next = newNode;
      cur = newNode.next;
    }
    cur = head;
    while (cur != null) { // 设置新节点的随即指针指向
      if (cur.random != null) { // 排除 random 为 null 的情况
        cur.next.random = cur.random.next;
      }
      cur = cur.next.next;
    }
    cur = head;
    Node pre = head.next, res = head.next;
    while (pre.next != null) { // 拆分链表
      cur.next = cur.next.next;
      pre.next = pre.next.next;
      cur = cur.next;
      pre = pre.next;
    }
    cur.next = null; // 注意链表末端并没有拆开呢！
    return res;
  }
}

✔️Day 3

刷题笔记：《剑指 Offer 第三天》

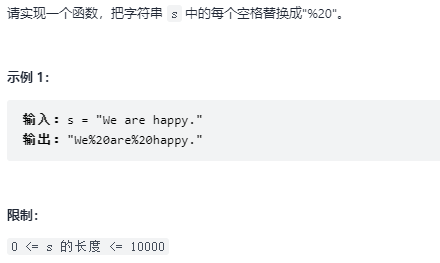
05. 替换空格

题目：剑指 Offer 05. 替换空格

剑指 Offer 05

解题思路

使用 StringBuilder，注意字符串拼接使用 StringBuilder 要比使用 StringBuffer 更好，因为 StringBuffer 底层加了锁，是线程安全的，但是会消耗一定的性能。

简单字符串拼接使用 + 拼接性能和使用 StringBuilder 差不多，自 JDK 1.5 开始，Java 编译器就做了优化，使用 + 拼接字符串，编译器编译后实际就自动优化为使用 StringBuilder。

使用循环拼接时，每次循环都会 new 一个 StringBuilder 对象，这时使用 StringBuilder 会更好；

注意： StringBuilder 不是线程安全的！！！StringBuffer 是线程安全的！！

算法流程

遍历字符串的每个字符然后使用 StringBuilder 拼接即可；

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
  public String replaceSpace(String s) {
    StringBuilder builder = new StringBuilder();
    char c;
    for(int i = 0; i < s.length(); ++i) {
      c = s.charAt(i);
      if(c == ' ') {
        builder.append("%20");
      } else {
        builder.append(c);
      }
    }
    return builder.toString();
  }
}

58 - II. 左旋转字符串

题目：剑指 Offer 58 - II. 左旋转字符串

剑指 Offer 58

由于 Java 在循环中字符串拼接都是新 new 了一个对象，所以直接使用 String 内存空间消耗较大，采用 StringBuilder 对象拼接字符串；

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
  public String reverseLeftWords(String s, int n) {
    StringBuilder builder = new StringBuilder();
    for (int i = n; i < s.length(); ++i) {
      builder.append(s.charAt(i));
    }
    for (int i = 0; i < n ;++i) {
      builder.append(s.charAt(i));
    }
    return builder.toString();
  }
}

解题代码-优化？（代码简洁了，但是似乎耗时更多了）

1
2
3
4
5
6
7
8
9
class Solution {
  public String reverseLeftWords(String s, int n) {
    StringBuilder builder = new StringBuilder();
    for (int i = n; i < s.length() + n; ++i) {
      builder.append(s.charAt(i % s.length()));
    }
    return builder.toString();
  }
}

✔️Day 4

刷题笔记：《剑指 Offer 第四天》

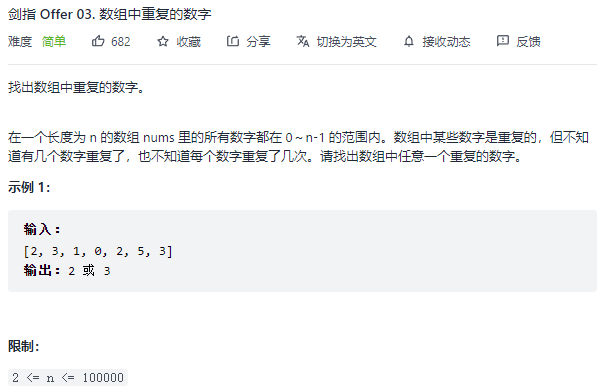
03. 数组中重复的数字

题目：剑指 Offer 03. 数组中重复的数字

剑指 Offer 03

解题思路

构建一个计数数组 count，刚开始通过 nums 数组中的值作为 计数数组 count 的索引去进行计数，但是突然发现 n 的值有点大，最坏情况下需要开十万的数组（2 <= n <= 100000），太消耗内存空间了！

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
  // 优化了一点点，内存空间占用少，耗时高
  public int findRepeatNumber(int[] nums) {
    int[] count = new int[nums.length];
    for (int i = 0; i < count.length; ++i) {
      if (count[nums[i]] != 0) {
        return nums[i];
      }
      count[nums[i]]++;
    }
    return -1;
  }
}

题解解法

算法流程

  1. 遍历数组 numsnums ，设索引初始值为 i = 0:
    1. 若 nums[i] = i： 说明此数字已在对应索引位置，无需交换，因此跳过；
    2. 若 nums[nums[i]] = nums[i]： 代表索引 nums[i] 处和索引 ii 处的元素值都为 nums[i]，即找到一组重复值，返回此值 nums[i]；
    3. 否则： 交换索引为 i 和 nums[i] 的元素值，将此数字交换至对应索引位置。
  2. 若遍历完毕尚未返回，则返回 −1 。

复杂度分析

  • 时间复杂度 O(N) ： 遍历数组使用 O(N) ，每轮遍历的判断和交换操作使用 O(1) 。
  • 空间复杂度 O(1) ： 使用常数复杂度的额外空间。

题解代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
  // 内存空间占用略高，耗时低
  public int findRepeatNumber(int[] nums) {
    int i = 0;
    while(i < nums.length) {
      if(nums[i] == i) {
        i++;
        continue;
      }
      if(nums[nums[i]] == nums[i]) return nums[i];
      // 交换 nums[i] 与 nums[nums[i]]
      int tmp = nums[i];
      nums[i] = nums[tmp];
      nums[tmp] = tmp;
    }
    return -1;
  }
}

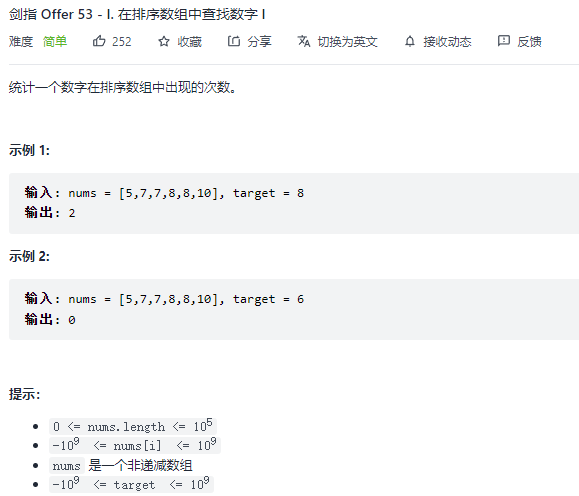
53 - I. 在排序数组中查找数字 I

题目：剑指 Offer 53 - I. 在排序数组中查找数字 I

剑指 Offer 53 - 1

解题思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class Solution {
  public static void main(String[] args) {
    System.out.println(search((new int[]{2,2}),2));
  }
  // 使用二分查找找到一个匹配元素，以此元素为基准去左右探测相同元素并计数
  public static int search(int[] nums, int target) {
    if (nums.length == 0) { // [] 特例处理
      return 0;
    }
    // 注意右边界是 length - 1，否则容易越界！
    int begin = 0, end = nums.length - 1;
    while (begin <= end) {
      int mid = begin + (end - begin) / 2;
      if (nums[mid] == target) {
        int count = 1;
        // 向左探测
        for (int i = mid - 1; i >= begin; --i) {
          if (mid == 0 || nums[i] != target) {
            // 防止 mid 边界上导致 mid - 1 越界
            break;
          }
          count++;
        }
        // 向右探测
        for (int i = mid + 1; i <= end; ++i) {
          if (i >= nums.length || nums[i] != target) {
            // 防止 mid 边界上导致 mid + 1 越界
            break;
          }
          count++;
        }
        return count;
      } else if (nums[mid] < target){
        begin = mid + 1;
      } else {
        end = mid - 1;
      }
    }
    return 0;
  }
  /**
   * 二分查找算法递归实现
   */
  public int binary_search(int[] nums, int start, int end, int target) {
    if (start > end) {
      return -1;
    }
    int mid = start + (end - start) / 2;
    if (target == nums[mid]) {
      return mid;
    }
    if (target < nums[mid]) {
      return binary_search(nums, start, mid - 1, target);
    }
    // target > nums[mid]
    return binary_search(nums, mid, end, target);
  }
}

53 - II. 0～n-1中缺失的数字

题目：剑指 Offer 53 - II. 0～n-1中缺失的数字

Offer 53 - 2

解题思路

高斯求和公式，做差即可，时间复杂度 O(N)

1
2
3
4
5
6
7
8
9
10
public class Solution {

  public int missingNumber(int[] nums) {
    int len = nums.length, sum = 0;
    for (int num : nums) {
      sum += num;
    }
    return (len + 1) * (len) / 2 - sum; // 高斯求和公式 0 ~ (n - 1)
  }
}

使用 异或操作，相同元素 ^ = 0（1 ^ 1 = 0 ），无本质区别，时间复杂度都是 O(N)

1
2
3
4
5
6
7
8
9
10
11
class Solution {
  public static int missingNumber(int[] nums) {
    // 这题我写过！
    for (int i = 0 ; i < nums.length; ++i) {
      if ((nums[i] ^ i) != 0) { // 异或操作 1 ^ 1 = 0
        return i;
      }
    }
    return nums.length; // 特例：[0] []
  }
}

题解思路

使用二分法，可以将复杂度降低至 log(N)，后补！

✔️Day 5

刷题笔记：《剑指 Offer 第五天》

04. 二维数组中的查找

题目：剑指 Offer 04. 二维数组中的查找

剑指 Offer 04

解题思路

从右上角开始遍历，右上角的元素具有以下性质：

  1. 它是该行最大的元素
  2. 它是该列最小的元素

通过带查找元素 target 与 这个元素比较可以主键缩小列与行；

时间复杂度 O(N M)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public boolean findNumberIn2DArray(int[][] matrix, int target) {
  if (matrix == null || matrix.length == 0) {
    return false;
  }
  // row -> 行   col -> 列
  int row = 0, col = matrix[0].length - 1;
  while (row < matrix.length && col >= 0) {
    if (matrix[row][col] > target) {
      col--;
    } else if (matrix[row][col] < target){
      row++;
    } else {
      return true;
    }
  }
  return false;
}

11. 旋转数组的最小数字

题目：剑指 Offer 11. 旋转数组的最小数字

剑指 Offer 11

解题思路

参数数组 numbers 的构成是 A + B，A、B分别是升序数组，且有 Max(B) <= Min(A)；可以从数组末端遍历数组，找到比左端元素小的那个元素即为 B 的第一个元素，也就是最小元素；

解题代码

1
2
3
4
5
6
7
8
9
10
class Solution {
  public int minArray(int[] numbers) {
    for (int i = numbers.length - 1; i > 0; --i) {
      if (numbers[i] < numbers[i - 1]) {
        return numbers[i];
      }
    }
    return numbers[0]; // 特例，没有旋转
  }
}

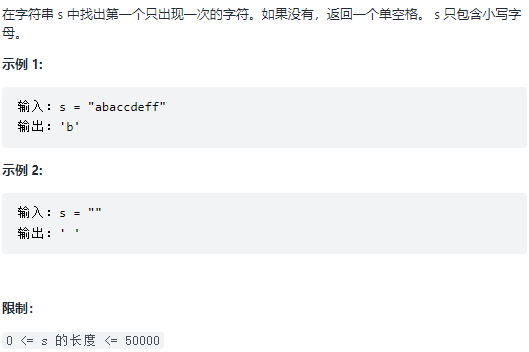
50. 第一个只出现一次的字符

题目：剑指 Offer 50. 第一个只出现一次的字符

剑指 Offer 50

解题思路

刚开始构建了 计数数组cout，但是后来发现与题目不太一样，技术数组只能统计个数，不能满足题干中 第一个 这个条件，后来考虑使用 Hash 表，遍历两次，第一次遍历找出只出现一次的字符，第二次找出第一个只出现一次的字符

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
  public char firstUniqChar(String s) {
    if (s.equals("")) return ' ';
    Map<Character, Boolean> map = new HashMap();
    char c;
    Boolean exist;
    // 一次遍历字符串，构建哈希表
    for (int i = 0; i < s.length(); ++i) {
      c = s.charAt(i);
      exist = map.get(c);
      if (null == exist) {
        map.put(c, true);
        continue;
      }
      if(map.get(c)) {
        map.put(c, false);
      }
    }
    // 二次遍历字符串，找到第一个出现一次的字符
    for (int i = 0; i < s.length(); ++i) {
      c = s.charAt(i);
      if (map.get(c)) return c;
    }
    return ' ';
  }
}

题解

在哈希表的基础上，有序哈希表中的键值对是 按照插入顺序排序 的。基于此，可通过遍历有序哈希表，实现搜索首个 “数量为 1 的字符”。

哈希表是 去重 的，即哈希表中键值对数量字符串 s 的长度。因此，相比于方法一，方法二减少了第二轮遍历的循环次数。当字符串很长（重复字符很多）时，方法二则效率更高。

在 Java 中有有序哈希表，可以少遍历一次字符串，Map<Character, Boolean> map = new LinkedHashMap();

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
  public char firstUniqChar(String s) {
    if (s.equals("")) return ' ';
    Map<Character, Boolean> map = new LinkedHashMap<>();
    char[] chs = s.toCharArray();
    for (char ch : chs) {
      map.put(ch, !map.containsKey(ch));
    }
    for (Map.Entry<Character, Boolean> d : map.entrySet()) {
      if (d.getValue()) return d.getKey();
    }
    return ' ';
  }
}

✔️Day 6

刷题笔记：《剑指 Offer 第六天》

面试题32 - I. 从上到下打印二叉树

题目：面试题32 - I. 从上到下打印二叉树

剑指 Offer 32 - 1

解题思路

  • 从上至下 打印（按层打印）二叉树，又称为二叉树的 广度优先搜索 (BFS)；
  • BFS 通常借助 队列 的先入先出特性来实现；

算法流程

  1. 特例处理： 根节点为空，直接返回空数组 []；
  2. 初始化： 打印结果列表 res = []，包含根节点的队列 queue = [root] ；
  3. BFS 循环： 当前队列 queue 为空时结束循环；
    1. 出队： 队首出队，记为 node；
    2. 打印： 将 node.val 添加至动态数组 ans 的尾部；
    3. 添加子节点： 若 node 有左（右）节点，则按照先左后右的顺序将子节点添加至队列 queue；
  4. 返回值： 返回打印结果列表 res 即可

复杂度分析

  • 时间复杂度 O(N)： N 为二叉树的节点数量，即 BFS 需循环 N 次
  • 空间复杂度 O(N)： 最差情况下，即当树为平衡二叉树时，最多有 N/2 个树节点 同时 在 queue 中，使用 O(N) 大小的额外空间

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class Solution {
  public int[] levelOrder(TreeNode root) {
    if (root == null) { // 特列：空树
      return new int[0];
    }
    Queue<TreeNode> queue = new LinkedList<>();
    // Queue 使用时要尽量避免 add 和 remove 方法，用 offer 和 poll 来加入和移除元素；
    queue.offer(root); // 根节点入队
    ArrayList<Integer> ans = new ArrayList<>(); // 不确定节点数量，采用动态数组添加节点值
    while (!queue.isEmpty()) {
      TreeNode node = queue.poll(); // 先进先出
      ans.add(node.val); // 取出当前节点的值
      if(node.left != null) { // 把左节点进队
        queue.offer(node.left);
      }
      if(node.right != null) { // 把右节点进队
        queue.offer(node.right);
      }
    }
    // 将 ArrayList 转为 int数组并返回
    int[] res = new int[ans.size()];
    for(int i = 0; i < ans.size(); i++) {
      res[i] = ans.get(i);
    }
    return res;
  }
}

32 - II. 从上到下打印二叉树 II

题目：剑指 Offer 32 - II. 从上到下打印二叉树 II

剑指 Offer 32 - 2

解题思路

这道题和 面试题32 - I. 从上到下打印二叉树 基本一样，把面试题32的代码写出来之后就没了思路，正在想队列一次只能出队一个，怎么对元素分层打印涅，突然就看到了 queue.size()；牛🐂！

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class Solution {
  public List<List<Integer>> levelOrder(TreeNode root) {
    Queue<TreeNode> queue = new LinkedList<>();
    if (root != null) {
      queue.offer(root);
    }
    List<List<Integer>> res = new ArrayList<>();
    while (!queue.isEmpty()) {
      List<Integer> list = new ArrayList<>();
      // 每次打印上次队列中的元素个数
      for (int i = queue.size(); i > 0; --i) {
        TreeNode node = queue.poll();
        list.add(node.val);
        if (node.left != null) {
          queue.offer(node.left);
        }
        if (node.right != null) {
          queue.offer(node.right);
        }
      }
      res.add(list);
    }
    return res;
  }
}

32 - III. 从上到下打印二叉树 III

题目：剑指 Offer 32 - III. 从上到下打印二叉树 III

剑指 Offer 32 - 3

解题思路

都是面试题32-I 的同类型题（甚至可以说是一个题，输出格式不同 0.0），这个题个人思路加个变量统计判断奇偶决定队列顺序即可，后来实现代码后发现不太行，因为这样之后队列中下次遍历的元素与上次便利的元素有关联，比如：

[1, 2, 3, 4, null, null, 5]，按照上述想法得出结果是：[[1], [3, 2], [5, 4]]，与预期结果 [[1], [3, 2], [4, 5]] 结果不符合；

后来转变思路，其他部分照旧，在加入 list 前做奇偶判断，选择是否逆置数组；

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public static List<List<Integer>> levelOrder(TreeNode root) {
  Queue<TreeNode> queue = new LinkedList<>();
  if (root != null) {
    queue.offer(root);
  }
  List<List<Integer>> res = new ArrayList<>();
  int count = 0;
  while (!queue.isEmpty()) {
    count++;
    List<Integer> list = new ArrayList<>();
    for (int i = queue.size(); i > 0; --i) {
      TreeNode node = queue.poll();
      list.add(node.val);
      if (node.left != null) {
        queue.offer(node.left);
      }
      if (node.right != null) {
        queue.offer(node.right);
      }
    }
    if ((count & 1) == 1) {
      res.add(list);
    } else {
      List<Integer> reverseList = new ArrayList<>();
      for (int i = list.size() - 1; i >= 0 ; --i) {
        reverseList.add(list.get(i));
      }
      res.add(reverseList);
    }
  }
  return res;
}

题解

看了大佬的题解，ArrayList 提供了一些插入方法，可以直接进行尾插，我们可以在判断奇数偶数后进行头插操作；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public static List<List<Integer>> levelOrder(TreeNode root) {
  Queue<TreeNode> queue = new LinkedList<>();
  if (root != null) {
    queue.offer(root);
  }
  List<List<Integer>> res = new ArrayList<>();
  int count = 0;
  while (!queue.isEmpty()) {
    count++;
    LinkedList<Integer> list = new LinkedList<>();
    for (int i = queue.size(); i > 0; --i) {
      TreeNode node = queue.poll();
      if ((count & 1) == 1) { // 奇数层
        list.addLast(node.val);
      } else { // 偶数层，需要从右到左，采用头插法
        list.addFirst(node.val);
      }
      if (node.left != null) {
        queue.offer(node.left);
      }
      if (node.right != null) {
        queue.offer(node.right);
      }
    }
    res.add(list);
  }
  return res;
}

✔️Day 7

刷题笔记：《剑指 Offer 第七天》

26. 树的子结构

题目：https://leetcode-cn.com/problems/shu-de-zi-jie-gou-lcof/

剑指 Offer 26

解题思路

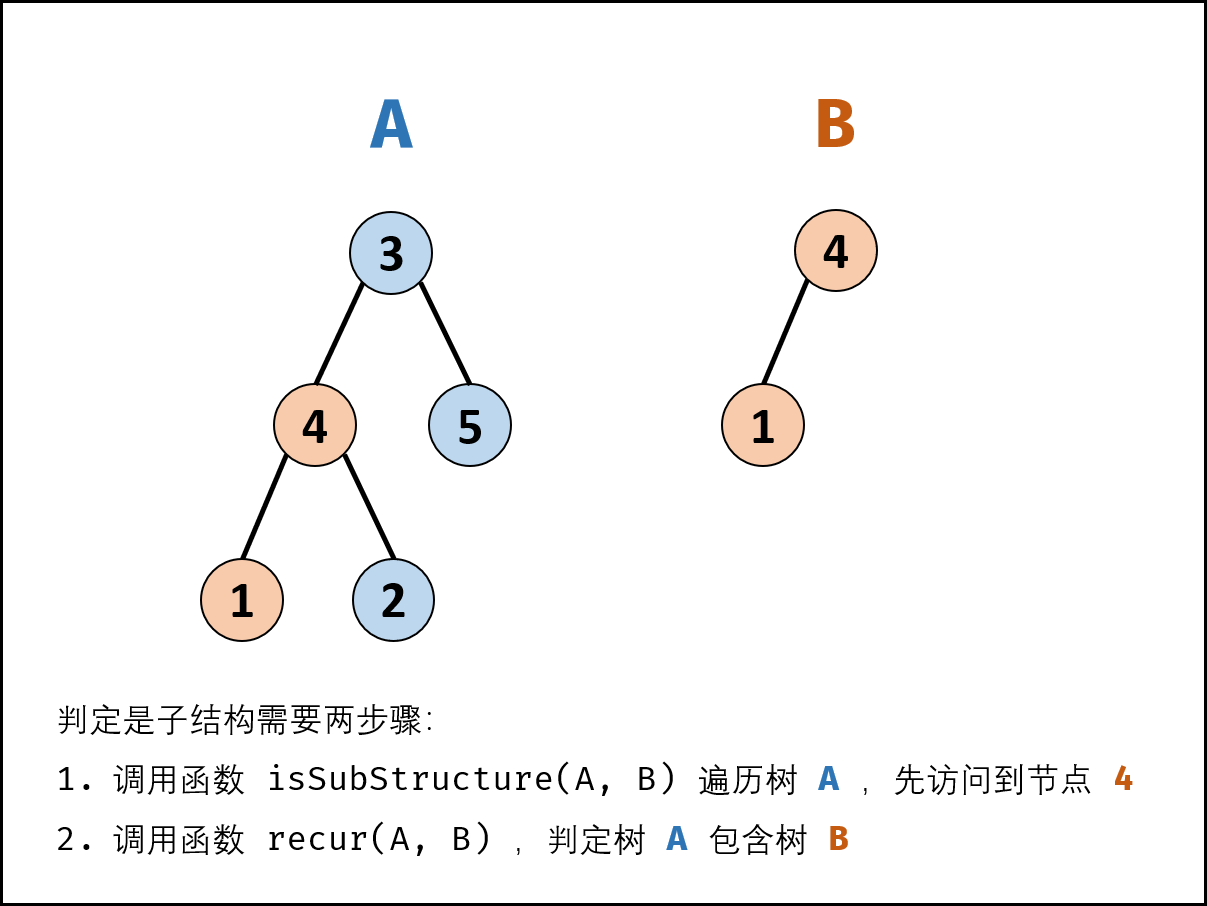
若树 B 是树 A 的子结构，则子结构的根节点可能为树 A 的任意一个节点，因此，判断树 B 是否是树 A 的子结构，需要完成以下两部工作：

  1. 先序遍历树 A 中的每个节点 n~A~；（对应函数 isSubStructure(A, B)）
  2. 判断树 A 中 以 n~A~ 为根节点的子树 是否包含树 B ；（对应函数 isSub(A, B)）

leetcode krehats 图解

复杂度分析

  • 时间复杂度 O(MN)：其中 M，N 分别为 树 A 和 树 B 的节点数量； 先序遍历 树 A 占用 O(M)，每次调用 isSub(A, B) 判断占用 O(N)；
  • 空间复杂度 O(M)：当 树 A 和 树 B 都退化为链表时，递归调用深度最大，当 M <= N 时，遍历 树 A 与递归判断的总递归深度为 M； 当 M > N 时，最差情况遍历至 树 A 叶子节点，此时递归深度为 M；

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
  public boolean isSubStructure(TreeNode A, TreeNode B) {
    if (A == null || B == null) {
      return false;
    } 
    return isSub(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
  }
  public boolean isSub(TreeNode A, TreeNode B) {
    if (B == null) {
      return true;
    }
    if (A == null || A.val != B.val) {
      return false;
    }
    return isSub(A.left, B.left) && isSub(A.right, B.right);
  }
}

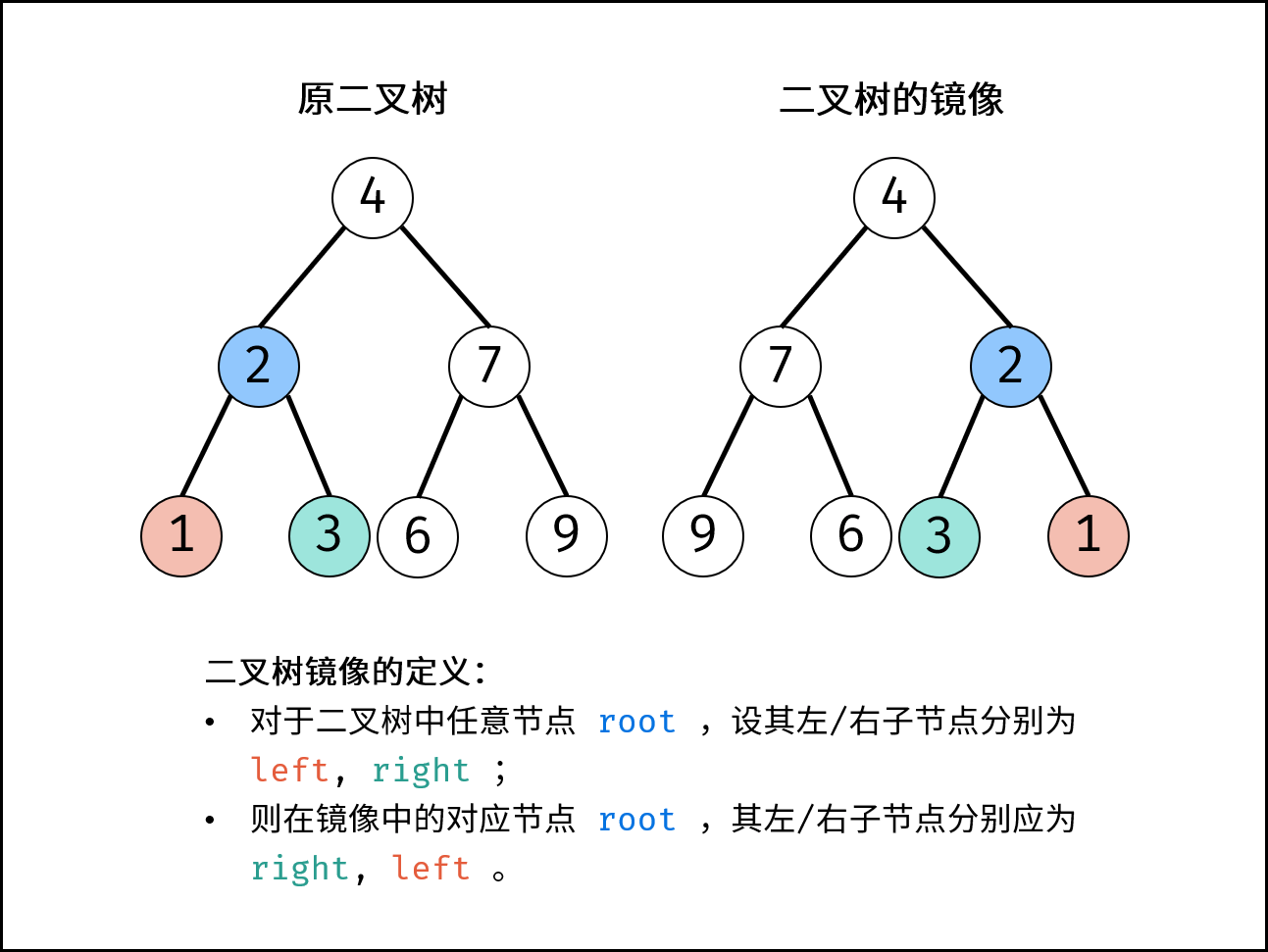
27. 二叉树的镜像

题目：剑指 Offer 27. 二叉树的镜像

剑指 Offer 27

解题思路

leetcode krehats 图解

递归 dfs 遍历二叉树，交换每个节点的左右子节点，即可生成二叉树的镜像；

Q： 为何需要暂存 root 的左子节点？

A： 在递归右子节点 root.left = mirrorTree(root.right) 执行完毕后， root.left 的值已经发生改变，此时递归左子节点 mirrorTree(root.left) 则会出问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
  public TreeNode mirrorTree(TreeNode root) {
    if (root == null) {
      return root;
    }
    TreeNode tmp = root.left;
    root.left = mirrorTree(root.right);
    root.right = mirrorTree(tmp);
    // 便于理解版本：
    // TreeNode leftRoot = mirrorTree(root.right);
    // TreeNode rightRoot = mirrorTree(root.left);
    // root.left = leftRoot
    // root.right = rightRoot
    return root;
  }
}

28. 对称的二叉树

题目：剑指 Offer 28. 对称的二叉树

剑指 Offer 28

解题思路

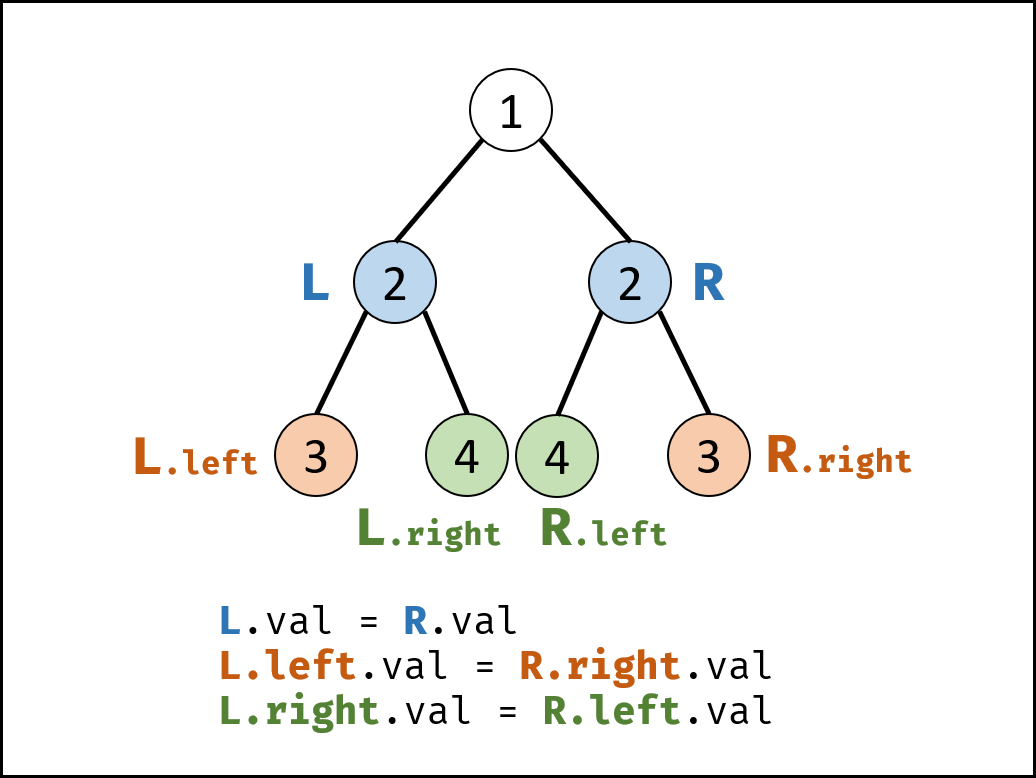
对于一个二叉树的任意两个对称的节点 L、R，其镜像的前提是：

  1. L.val = R.val
  2. L.left.val = R.right.val
  3. L.right.val = R.left.val

leetcode krehats 图解

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Solution {
  public boolean isSymmetric(TreeNode root) {
    return root == null || isSub(root.left, root.right);
  }
  public boolean isSub(TreeNode A, TreeNode B) {
    if (A == null && B == null ) {
      return true;
    }
    if (A == null || B == null || A.val != B.val) {
      return false;
    }
    return isSub(A.left, B.right) && isSub(A.right, B.left);
  }
}

✔️Day 8

刷题笔记：《剑指 Offer 第八天》

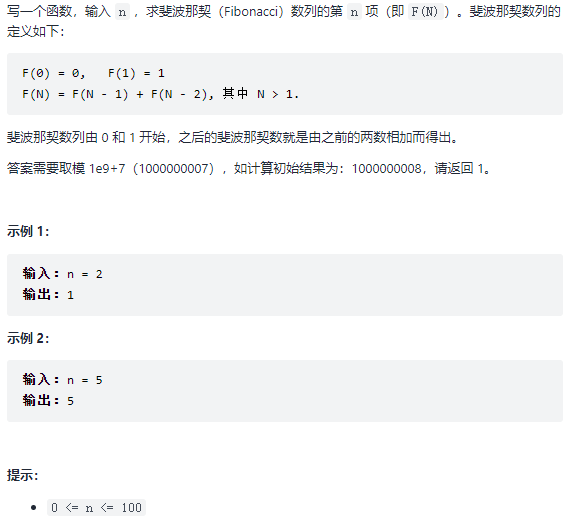
10- I. 斐波那契数列

题目：剑指 Offer 10- I. 斐波那契数列

剑指 Offer 10 - 1

解题思路

很容易推导出递归式：f(n + 1) = f(n) + f(n - 1)，然后使用递归，啪的一下，很快啊，爆栈了 qaq；

使用动态规划求解：

  1. 状态定义：dp[i] 表示斐波那契数列中的第 i 个数；
  2. 递归方程：dp[i + 1] = dp[i] + dp[i - 1]
  3. 初始状态：dp[0] = 0, dp[1] = 1
  4. 返回值：dp[n]

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
  private final int mod = 1000000007;
  public int fib(int n) {
    if (n < 2) {
      return n;
    }
    int[] dp = new int[n + 1];
    dp[0] = 0;
    dp[1] = 1;
    for (int i = 2; i <= n; ++i) {
      dp[i] = (dp[i - 1] + dp[i - 2]) % mod;
    }
    return dp[n];
  }
}

由于 dp[n] 只和 dp[n - 1] 和 dp[i - 2] 有关，所以可以节省数组空间，循环递推；

解题思路—优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution2 {
  private final int mod = 1000000007;
  public int fib(int n) {
    if (n <= 1) {
      return n;
    }
    int p = 0, q = 1, sum;
    for (int i = 0; i < n; ++i) {
      sum = (p + q) % mod;
      p = q;
      q = sum;
    }
    return p;
  }
}

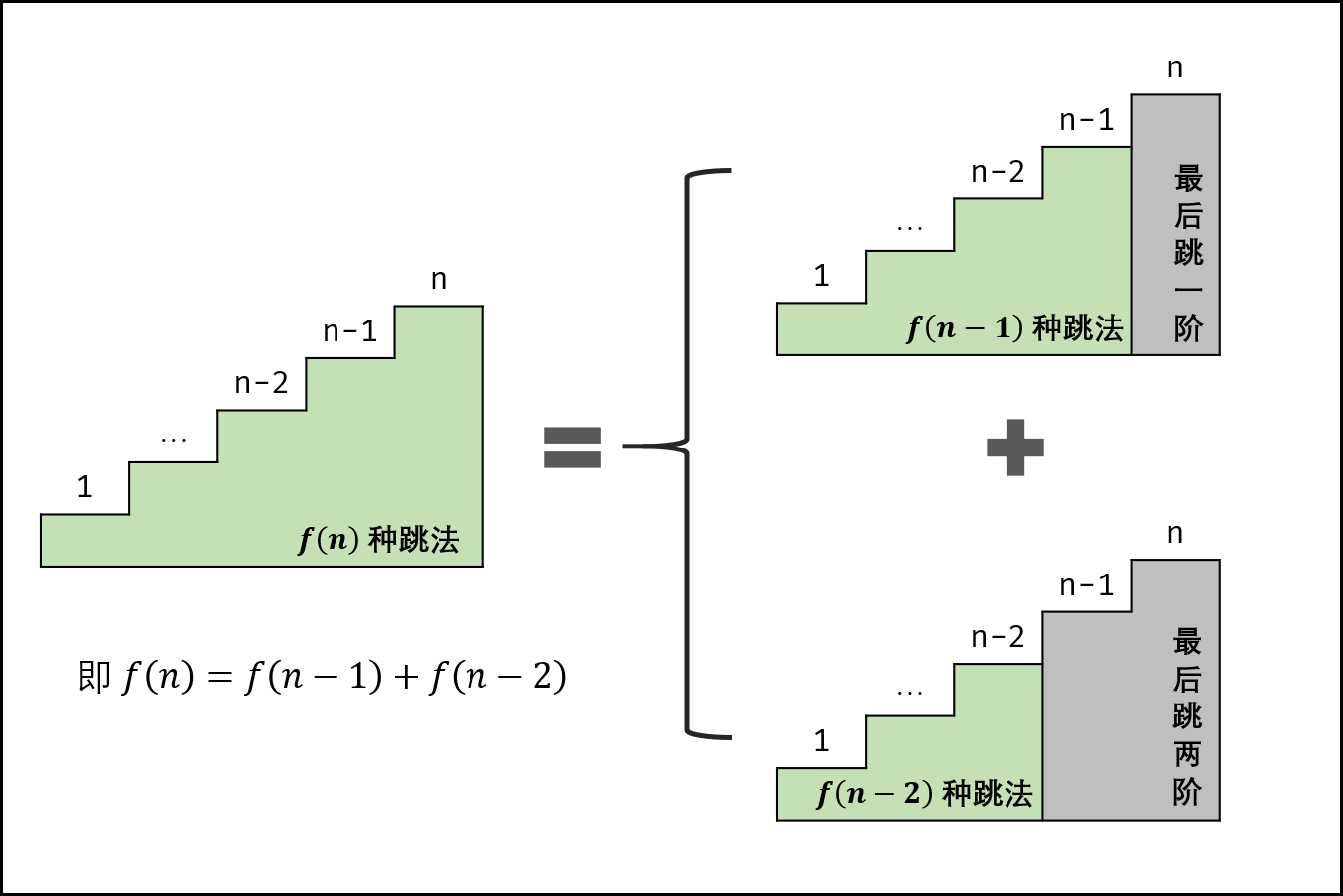
10- II. 青蛙跳台阶问题

题目：剑指 Offer 10- II. 青蛙跳台阶问题

剑指 Offer 10 - 2

解题思路

基本上和斐波那契数那题一样，唯一区别就是初始状态不太一样了；

leetcode krehats 图解

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {
  private final int mod = 1000000007;
  public int numWays(int n) {
    if (n < 2) {
      return 1;
    }
    int p = 1, q = 1, sum = 1;
    for (int i = 2; i <= n; ++i) {
      p = q;
      q = sum;
      sum = (p + q) % mod;
    }
    return sum;
  }
}

63. 股票的最大利润

题目：剑指 Offer 63. 股票的最大利润

剑指 Offer 63

解题思路

一样动态规划求解，dp[i] 代表前 i 天可以获得的最大利润；可以得知 dp[0] = 0；可以得到转移方程：dp[i] = max(dp[i - 1], prices[i] - min(prices[0, i - 1]))

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class Solution {
  public int maxProfit(int[] prices) {
    if (prices.length == 0) {
      return 0;
    }
    int[] dp = new int[prices.length];
    dp[0] = 0;
    for (int i = 1; i < prices.length; ++i) {
      dp[i] = Math.max(dp[i - 1], prices[i] - min(prices, i));
    }
    return dp[prices.length - 1];
  }
  /**
   * 数组 arr 前 size 项的最小值
   */
  public int min(int[] arr, int size) {
    int min = Integer.MAX_VALUE;
    for (int i = 0; i < size; ++i) {
      if (arr[i] < min) {
        min = arr[i];
      }
    }
    return min;
  }
}

解题代码—优化

看了题解优化了一点点，利用一个变量记录前 i 项的最小值，不必每次调用自定义 min 函数了，省了很多时间！208 ms 41.1MB -> 2 ms 41.7MB

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {
  public int maxProfit(int[] prices) {
    if (prices.length == 0) {
      return 0;
    }
    int[] dp = new int[prices.length];
    dp[0] = 0;
    int min = prices[0];
    for (int i = 1; i < prices.length; ++i) {
      min = Math.min(min, prices[i]);
      dp[i] = Math.max(dp[i - 1], prices[i] - min);
    }
    return dp[prices.length - 1];
  }
}

解题代码—再优化

2ms 41.7 MB -> 1 ms 41.2MB

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution { // 又优化了一点点，省去了数组的空间，空间复杂度降为 O(1)
  public int maxProfit(int[] prices) {
    if (prices.length < 2) { // 特例：[] [1] 没有卖出的可能性
      return 0;
    }
    int min = prices[0];
    // p 代表前 i 天的最大利润，初始为 0
    // q 代表第 i + 1 天的最大利润
    int p = 0, q;
    for (int i = 1; i < prices.length; ++i) {
      min = Math.min(min, prices[i]);
      q = Math.max(p, prices[i] - min);
      p = q;
    }
    return p;
  }
}

解题代码—还能优化

1ms 41.2MB -> 0ms 41.1 MB

1
2
3
4
5
6
7
8
9
10
class Solution { // 每次记录股票的最低价以及利润
  public int maxProfit(int[] prices) {
    int cost = Integer.MAX_VALUE, profit = 0;
    for(int price : prices) {
      cost = Math.min(cost, price);
      profit = Math.max(profit, price - cost);
    }
    return profit;
  }
}

✔️Day 9

刷题笔记：《剑指 Offer 第九天》

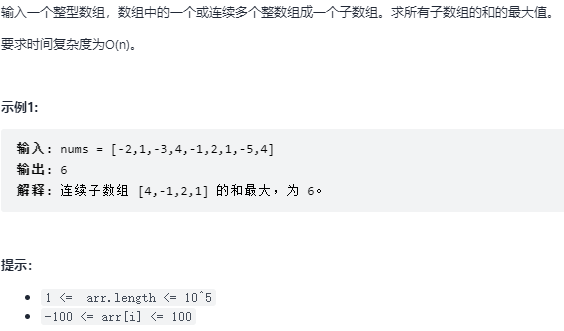
42. 连续子数组的最大和

题目：剑指 Offer 42. 连续子数组的最大和

剑指 Offer 42

解题思路

  • 状态定义：设动态规划列表 dp，dp[i] 代表以元素 nums[i] 结尾的连续子数组的最大和

  • 转移方程：若 dp[i - 1] ≤ 0，说明 dp[i - 1] 对 dp[i] 产生负贡献，即 dp[i - 1] + nums[i] ≤ nums[i] ；

  • 初始状态：dp[0] = nums[0]，即以 nums[0] 结尾的连续子数组的最大和为 nums[0]

  • 返回值：返回 dp 列表中的最大值，代表全局最大值

leetcode krehats 图解

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Solution {
  public int maxSubArray(int[] nums) {
    // 1. 状态定义：dp[i] 为以元素 nums[i] 结尾的连续子数组的最大和
    int[] dp = new int[nums.length];
    dp[0] = nums[0];
    // 2. 转移方程 dp[i] = nums[i] + (dp[i - 1] > 0 ? dp[i - 1] : 0)
    int max = nums[0];
    for (int i = 1; i < dp.length; ++i) {
      if (dp[i - 1] > 0) {
        dp[i] = nums[i] + dp[i - 1];
      } else {
        dp[i] = nums[i];
      }
      max = Math.max(max, dp[i]);
    }
    return max;
  }
}

解题代码—优化

dp[i] 只和 dp[i - 1] 和 nums[i] 有关系，因此可以在原数组上修改用作 dp 列表；

1
2
3
4
5
6
7
8
9
10
public class Solution { // k 神 题解版
  public int maxSubArray(int[] nums) {
    int res = nums[0];
    for(int i = 1; i < nums.length; i++) {
      nums[i] += Math.max(nums[i - 1], 0);
      res = Math.max(res, nums[i]);
    }
    return res;
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Solution { // 个人优化版
  public int maxSubArray(int[] nums) {
    int max = nums[0];
    int p = nums[0], q;
    for (int i = 1; i < nums.length; ++i) {
      if (p > 0) {
        q = nums[i] + p;
      } else {
        q = nums[i];
      }
      p = q;
      max = Math.max(max, q);
    }
    return max;
  }
}

47. 礼物的最大价值

题目：剑指 Offer 47. 礼物的最大价值

剑指 Offer 47

解题思路

分析题目可以得到如下的递推关系：f(i, j) = max[f(i - 1, j), f(i, j - 1)]

leetcode krehats 图解

  1. 状态定义：设动态规划矩阵 dp，dp[i][j] 表示从左上角走到单元格 (i, j) 的礼物最大累计价值

  2. 转移方程：

    1. 当 i = 0 且 j = 0 时，为起始元素；
    2. 当 i = 0 且 j ≠ 0 时，为矩阵第一行元素，只可从左边到达
    3. 当 i ≠ 0 且 j = 0 时，为矩阵第一列元素，只可从上边到达
    4. 当 i ≠ 0 且 j ≠ 0 时，可从左边或上边到达；

    $dp(i,j)= \begin{cases} grid(i,j) & {,i=0, j=0}\ grid(i,j) + dp(i,j-1) & {,i=0, j \ne 0}\ grid(i,j) + dp(i-1,j) & {,i \ne 0, j=0}\ grid(i,j) + \max[dp(i-1,j),dp(i,j-1)]& ,{i \ne 0, j \ne 0} \end{cases}$

  1. 初始状态：dp[0][0] = gird[0][0] ，即到达单元格 (0,0) 时能拿到礼物的最大累计价值为 grid[0][0]；

  2. 返回值：dp[m - 1][n - 1]，m，n 分别为矩阵的行高和列宽，即返回矩阵的右下角元素

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {
  public int maxValue(int[][] grid) {
    // 不管怎么选择，最终都是走了 m + n - 1 步
    /*
    *     grid     |      dp
    * 1    3    1  |  1    4    5
    * 1    5    1  |  2    9    10
    * 4    2    1  |  6    11   12
    * */
    int dp[][] = new int[grid.length][grid[0].length];
    for (int i = 0; i < grid.length; ++i) {
      for (int j = 0; j < grid[0].length; ++j) {
        if (i == 0 && j == 0) { // i == 0 && j == 0，即初始元素
          dp[i][j] = grid[i][j];
        } else if (i == 0) { // i == 0 && j != 0，第一行
          dp[i][j] = dp[i][j - 1] + grid[i][j];
        } else if (j == 0) { // i != 0 && j == 0，第一列
          dp[i][j] = dp[i - 1][j] + grid[i][j];
        } else { // 其他位置元素
          dp[i][j] = grid[i][j] + Math.max(dp[i - 1][j], dp[i][j - 1]);
        }
      }
    }
    return dp[dp.length - 1][dp[0].length - 1];
  }
}

题解代码-优化

由于 dp[i][j] 只与 dp[i-1][j] , dp[i][j-1] ，grid[i][j] 有关系，因此可以将原矩阵 grid 用作 dp 矩阵，即直接在 grid 上修改即可，可以将空间复杂度优化至 O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Solution2 {
  public int maxValue(int[][] grid) {
    int row = grid.length, col = grid[0].length;
    for (int i = 1; i < col; ++i) { // 初始化第一行
      grid[0][i] += grid[0][i - 1];
    }
    for (int i = 1; i < row; ++i) { // 初始化第一列
      grid[i][0] += grid[i - 1][0];
    }
    for (int i = 1; i < row; ++i) {
      for (int j = 1; j < col; ++j) {
        grid[i][j] += Math.max(grid[i - 1][j], grid[i][j - 1]);
      }
    }
    return grid[row - 1][col - 1];
  }

✔️Day 10

刷题笔记：《剑指 Offer 第十天》

46. 把数字翻译成字符串

题目：剑指 Offer 46. 把数字翻译成字符串

剑指 Offer 46

题解思路

根据题意总结出 “递推公式”，即转移方程，采用动态规划的方法解题；

leetcode krehats 图解

动态规划

记数字 num 第 i 位数字为 x~i~ ，数字 num 的位数为 n；

例如：num = 12283 的 n = 5，x~1~ = 1

  • 状态定义：动态规划列表 dp，dp[i] 代表以 x~i~ 结尾的数字的翻译方案数量
  • 转移方程：若 x~i~ 和 x~i-1~ 组成的两位数字可以被翻译（≥ 10 且 ≤ 25），则 dp[i] = dp[i - 1] + dp[i - 2]，否则 dp[i] = dp[i - 1]；
  • 初始状态：dp[0] = dp[1] = 1
  • 返回值：dp[n]，即此数字的翻译方案数量

解题代码

由于 dp[i] 仅仅和 dp[i -1] 有关，所以可以用两个变量来替代他们进行迭代即可；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class Solution {
  public int translateNum(int num) {
    String str = String.valueOf(num);
    // num = X1X2X3X4X5...
    // p, q 分别代表 dp[i] 和 dp[i - 1]; dp[i] 代表以 Xi 结尾的方案数
    int p = 1, q = 1;
    for (int i = 2; i <=str.length(); ++i) {
      String tmp = str.substring(i - 2, i);
      int sum; // sum 代表 dp[i + 1], 迭代中间量
      if (tmp.compareTo("10") >= 0 && tmp.compareTo("25") <= 0) {
        // dp[2] = dp[1] + dp[0];
        // dp[i] = dp[i - 1] + dp[i - 2];
        sum = p + q;
      } else {
        // dp[2] = dp[1];
        // dp[i] = dp[i - 1];
        sum = p;
      }
      q = p;
      p = sum;
    }
    return p;
  }
}

优化-求余

利用求余运算进一步减少 字符串 str 占用的空间复杂度 O(N) -> O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static int translateNum(int num) {
  // num = 12258
  int p = 1, q = 1, x, y = num % 10; // x 十位数，y 个位数
  while (num != 0) {
    num /= 10;
    x = num % 10;
    int tmp = x * 10 + y;
    int sum = tmp >= 10 && tmp <= 25 ? p + q : p;
    q = p;
    p = sum;
    y = x;
  }
  return p;
}

48. 最长不含重复字符的子字符串

题目：剑指 Offer 48. 最长不含重复字符的子字符串

剑指 Offer 48

解题思路

  • 状态定义： 设动态规划列表 dp，dp[j] 代表以字符 s[j] 为结尾的 “最长不重复子字符串” 的长度。

  • 转移方程： 固定右边界 j ，设字符 s[j] 左边距离最近的相同字符为 s[i]，即 s[i] = s[j]。

    1. 当 i < 0，即 s[j] 左边无相同字符，则 dp[j] = dp[j-1] + 1；

    2. 当 dp[j - 1] < j - i，说明字符 s[i] 在子字符串 dp[j−1] 区间之外，则 dp[j] = dp[j - 1] + 1；

    3. 当 dp[j−1] ≥ j − i，说明字符 s[i] 在子字符串 dp[j−1] 区间之中 ，则 dp[j] 的左边界由 s[i] 决定，即 dp[j] = j - i；

      当 i < 0i<0 时，由于 dp[j - 1] \leq jdp[j−1]≤j 恒成立，因而 dp[j - 1] < j - idp[j−1]<j−i 恒成立，因此分支 1. 和 2. 可被合并

  • 返回值： max(dp) ，即全局的 “最长不重复子字符串” 的长度。

leetcode krehats 图解

解题代码

  • 哈希表统计： 遍历字符串 s 时，使用哈希表统计 各个字符最后一次出现的索引
  • 左边界 i 获取方式： 遍历到 s[i] 时，可通过访问哈希表获取到最近的相同字符串的索引 j；
1
2
3
4
5
6
7
8
9
10
11
12
13
public class Solution {
  public int lengthOfLongestSubstring(String s) {
    int max = 0, tmp = 0;
    Map<Character, Integer> dic = new HashMap<>();
    for (int i = 0; i < s.length(); ++i) {
      int j = dic.getOrDefault(s.charAt(i), -1); // 获取索引 i
      dic.put(s.charAt(i), i); // 更新哈希表
      tmp = tmp < i - j ? tmp + 1 : i - j; // dp[j - 1] -> dp[j]
      max = Math.max(max, tmp); // max(dp[j - 1], dp[j])
    }
    return max;
  }
}

✔️Day 11

刷题笔记：《剑指 Offer 第十一天》

18. 删除链表的节点

题目：剑指 Offer 18. 删除链表的节点

剑指 Offer 18

解题思路

题目要求返回头节点，所以原先的头节点不能动；借助双指针完成更替操作，注意有个坑是需要删除的节点可能是头节点，此时需要改变头节点 head 的指向！

解题代码（双指针）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class Solution {
  public ListNode deleteNode(ListNode head, int val) {
    if (head == null) {
      return null;
    }
    ListNode cur = null, pre = head;
    while(pre != null) {
      if (pre.val == val) {
        if (cur == null) { // 需要删除的节点是头节点
          head = pre.next;
        } else {
          cur.next = pre.next;
        }
        // pre.next = null;
        break;
      }
      cur = pre;
      pre = pre.next;
    }
    return head;
  }
}

解题代码（单指针）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public ListNode deleteNode(ListNode head, int val) {
  if (head == null) { // 判空
    return null;
  }
  if (head.val == val) { // 需要删除的是头节点的情况
    return head.next;
  }
  ListNode pre = head;
  while(pre.next != null) {
    if (pre.next.val == val) {
      pre.next = pre.next.next;
      break;
    }
    pre = pre.next;
  }
 return head;
}

22. 链表中倒数第k个节点

题目：剑指 Offer 22. 链表中倒数第k个节点

剑指 Offer 22

解题代码

压栈后弹出 k - 1 个节点即可；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
  public ListNode getKthFromEnd(ListNode head, int k) {
    if (head == null) {
      return null;
    }
    Stack<ListNode> stack = new Stack<>();
    while (head != null) {
      stack.push(head);
      head = head.next;
    }
    while ((--k) > 0) {
      stack.pop();
    }
    // stack.get(k);
    return stack.pop();
  }
}

也可以借助 Java Stack 对象的方法 get

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
  public ListNode getKthFromEnd(ListNode head, int k) {
    if (head == null) {
      return null;
    }
    Stack<ListNode> stack = new Stack<>();
    while (head != null) {
      stack.push(head);
      head = head.next;
    }
    return stack.get(stack.size() - k);
  }
}

题解思路

可以考虑先遍历统计链表长度，记为 n ；设置一个指针走 (n-k) 步，即可找到链表倒数第 k 个节点。

使用双指针，前指针 pre 先走 k 步，然后 前后指针 cur、pre 一起走，当 pre == null 时，返回 cur 即可；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Solution2 {
  public ListNode getKthFromEnd(ListNode head, int k) {
    if (head == null || k == 0) {
      return null;
    }
    ListNode pre = head, cur = head;
    while ((k--) > 0) {
      pre = pre.next;
    }
    while (pre != null) {
      pre = pre.next;
      cur = cur.next;
    }
    return cur;
  }
}

✔️Day 12

刷题笔记：《剑指 Offer 第十二天》

25. 合并两个排序的链表

题目：剑指 Offer 25. 合并两个排序的链表

剑指 Offer 25

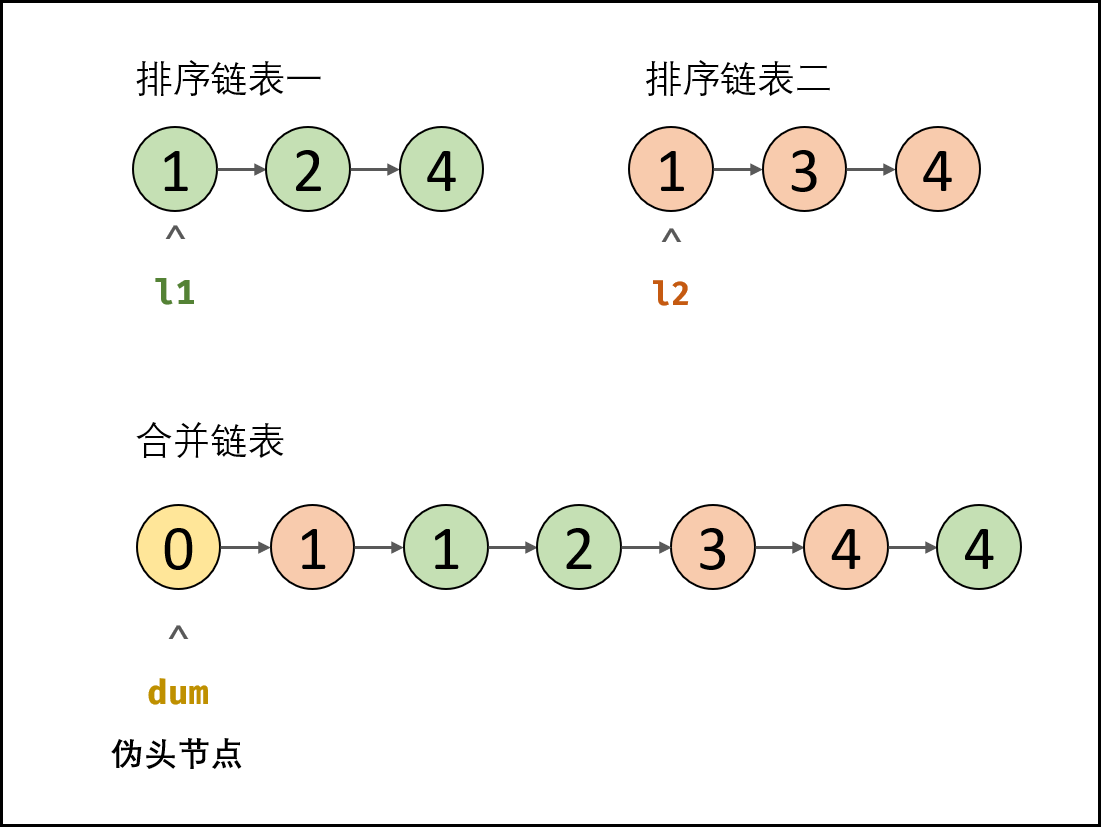
题解思路

自己想了半天，写了个错的！伤心，看了题解跟个人思路差不多，只能说大佬的图解太清晰了！链表的题目一定要自己画图，很容易出错！

引入伪头节点：由于初始状态合并链表中无节点，因此循环第一轮时无法将节点添加到合并链表中。解决方案：初始化一个辅助节点 dum 作为合并链表的伪头节点，将各节点添加至 dum 之后。

leetcode krehats 图解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class Solution {
  public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    if (l1 == null) {
      return l2;
    }
    if (l2 == null) {
      return l1;
    }
    // 构造一个假头节点
    ListNode head = new ListNode(0);
    ListNode cur = head;
    while (l1 != null && l2 != null) { // 短的链表节点遍历完跳出循环
      if (l1.val < l2.val) {
        cur.next = l1;
        l1 = l1.next;
      } else {
        cur.next = l2;
        l2 = l2.next;
      }
      cur = cur.next;
    }
    cur.next = l1 != null ? l1 : l2; // 合并长的链表的剩余节点
    return head.next;
  }
}

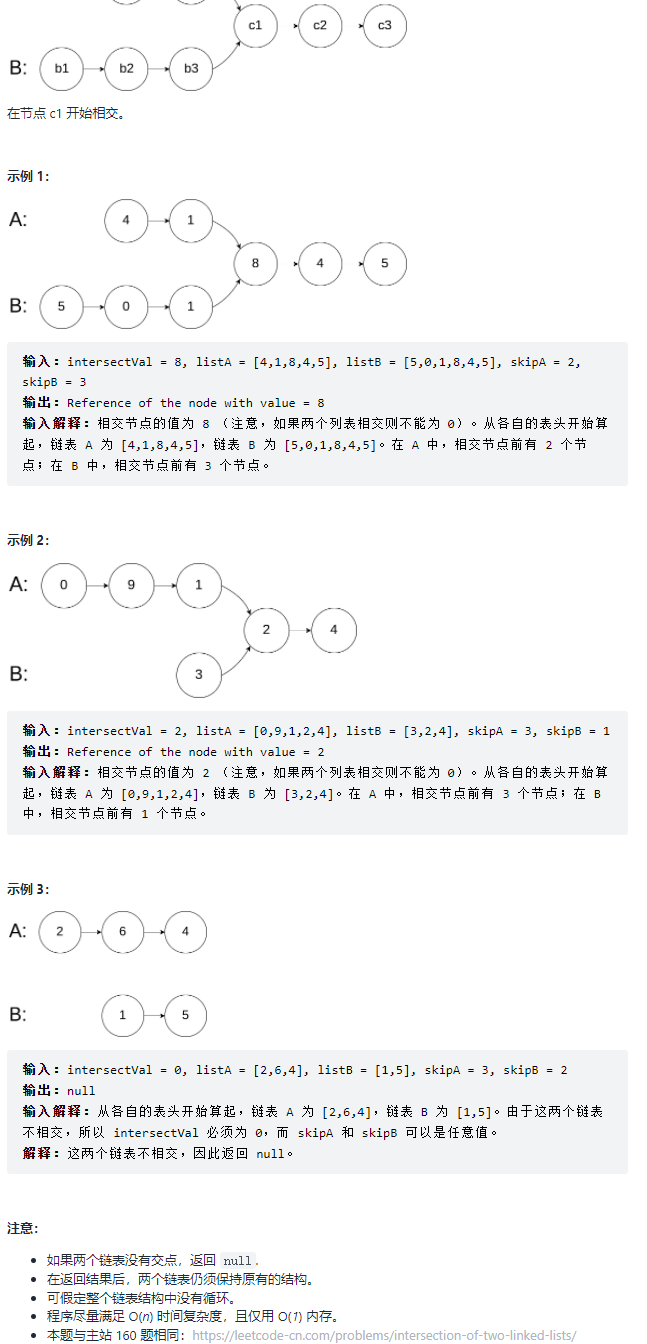
52. 两个链表的第一个公共节点

题目：剑指 Offer 52. 两个链表的第一个公共节点

剑指 Offer 52

解题思路

这题之前在 CS-Notes 这里刷过了，很巧妙的思路，通过拼接两个链表 l1、l2，让两个链表达到长度相同的情况（l1 + l2 = l2 + l1）从而继续遍历；

设 A 的长度为 a + c，B 的长度为 b + c，其中 c 为尾部公共部分长度，可知 a + c + b = b + c + a。

当访问链表 A 的指针访问到链表尾部时，令它从链表 B 的头部重新开始访问链表 B；同样地，当访问链表 B 的指针访问到链表尾部时，令它从链表 A 的头部重新开始访问链表 A。这样就能控制访问 A 和 B 两个链表的指针能同时访问到交点。

1
2
3
4
5
6
7
8
9
10
11
12
13
public class Solution {
  public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    if (headA == null || headB == null) { 
      return null;
    }
    ListNode l1 = headA, l2 = headB;
    while (l1 != l2) { // l1 == l2 || null == null
      l1 = l1 == null ? headB : l1.next;
      l2 = l2 == null ? headA : l2.next;
    }
    return l1;
  }
}

✔️Day 13

刷题笔记：《剑指 Offer 第十三天》

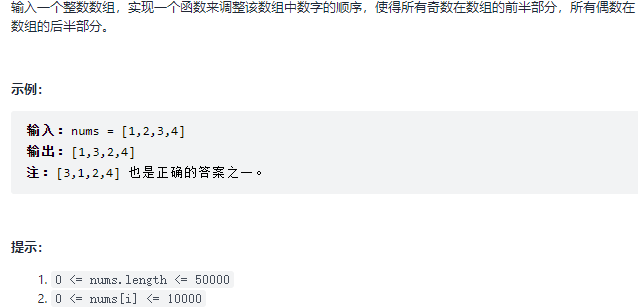
21. 调整数组顺序使奇数位于偶数前面

题目：剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

剑指 Offer 21

解题思路

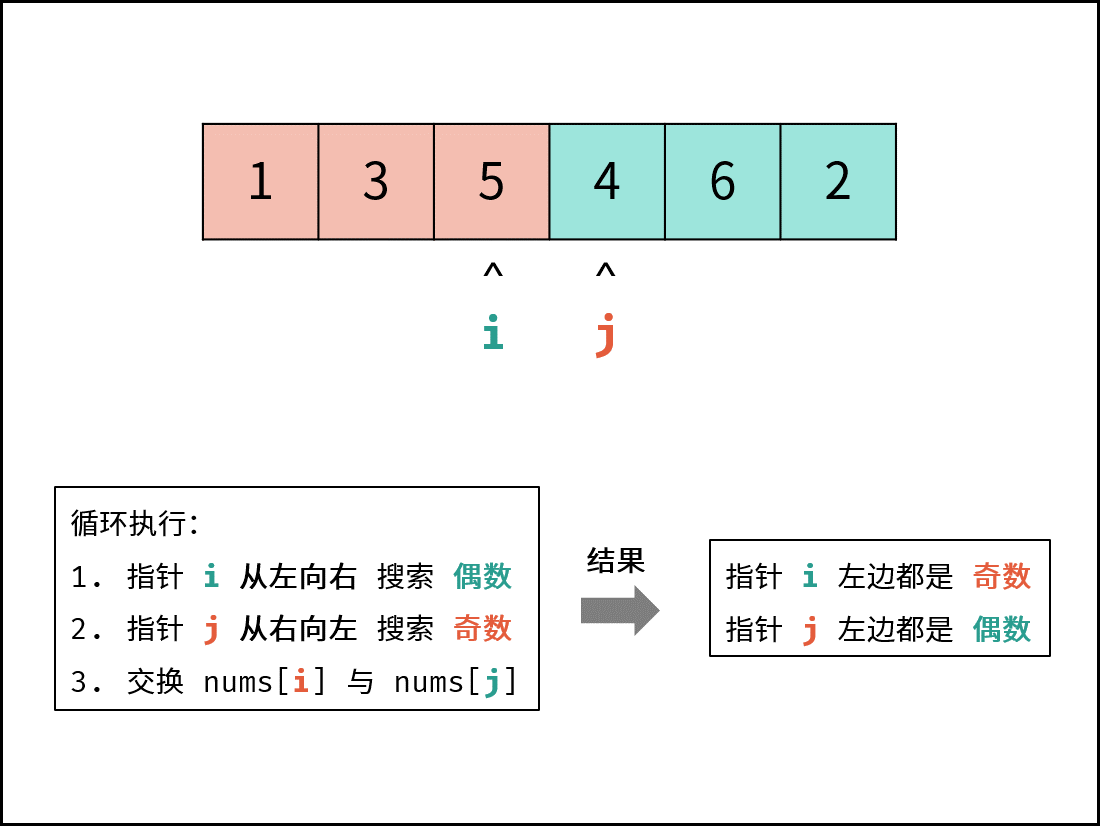
使用双指针遍历即可，指针 p 从头开始，指针 q 从末尾开始；执行下面的条件：

  1. nums[p] 是偶数；p++
  2. nums[q] 是奇数；q--
  3. nums[p] 是偶数且nums[q] 是奇数，交换 nums[p] 和 nums[q]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {
  public int[] exchange(int[] nums) {
    if (nums.length <= 1) {
      return nums;
    }
    int p = 0, q = nums.length - 1;
    while (p < q) {
      if ((nums[p] & 1) == 0 && (nums[q] & 1) == 1) { // 偶数、奇数 直接交换
        // a ^= b; b ^= a; a ^= b;
        nums[p] ^= nums[q];
        nums[q] ^= nums[p];
        nums[p] ^= nums[q];
        p++;
        q--;
      } else if ((nums[p] & 1) == 1 && (nums[q] & 1) == 0){ // 奇数、偶数
        p++;
        q--;
      } else if ((nums[p] & 1) == 1 && (nums[q] & 1) == 1) { // 奇数、奇数
        p++;
      } else { // 偶数、偶数
        q--;
      }
    }
    return nums;
  }
}

leetcode kerhats 图解

题解思路

难得跟题解思路差不多了一次，题解对代码优化了很多，使得代码更简洁了；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class Solution2 {
  public static void main(String[] args) {
    int[] ints = exchange(new int[]{2,4,6});
    // System.out.println(2^2);
    // System.out.println(2^0);
    // System.out.println(0^2);
    for (int i : ints) {
      System.out.println(i);
    }
  }
  public static int[] exchange(int[] nums) {
    if (nums.length <= 1) {
      return nums;
    }
    int p = 0, q = nums.length - 1, tmp;
    while (p < q) {
      while (p < q && (nums[p] & 1) == 1) { // p指针指的奇数
        p++;
      }
      while (p < q && (nums[q] & 1) == 0) { // q指针指的偶数
        q--;
      }
      // a ^= b; b ^= a; a ^= b; 这里有个 bug，有可能达到 p = q 的情况，此时用位运算会出错！
      tmp = nums[p];
      nums[p] = nums[q];
      nums[q] = tmp;
    }
    return nums;
  }
}

57. 和为s的两个数字

题目：剑指 Offer 57. 和为s的两个数字

剑指 Offer 57

解题思路

简单题写多了，看到第一时间就想暴力出奇迹了，时间复杂度 O(n^2^)

利用双指针可以解题，一个在左端，一个在右端，相遇则返回；

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution {
  public static int[] twoSum(int[] nums, int target) {
    int p = 0, q = nums.length - 1;
    while (p != q) {
      while (nums[p] + nums[q] < target) {
        p++;
      }
      while (nums[p] + nums[q] > target) {
        q--;
      }
      if (nums[p] + nums[q] == target) {
        return new int[]{nums[p], nums[q]};
      }
    }
    return new int[]{};
  }
}

写完发现可以进行一点点的优化，nums[p] + nums[q] 多次计算了，可以 new 一个 Integer 类型对象去存储它，空间换时间；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Solution {
  public static int[] twoSum(int[] nums, int target) {
    int p = 0, q = nums.length - 1, sum;
    while (p < q) {
      sum = nums[p] + nums[q];
      if (sum < target) {
        p++;
      } else if (sum > target) {
        q--;
      } else {
        return new int[]{nums[p], nums[q]};
      }
    }
    return new int[]{};
  }
}

因为此题是排序数组，所以可以进行这样的双指针操作，若不是排序数组，这样操作可能会导致丢失部分解；

日常借用 LeecCode K神 的图解：

图解

题解思路

也看到了利用二分法求解的，利用哈希表求解的，题解多种多样，再尝试一下哈希表求解的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Solution2 {
  public static int[] twoSum(int[] nums, int target) {
    Map<Integer, Integer> map = new HashMap<>();
    for (int num : nums) {
      map.put(num, num);
    }
    // 若哈希表中存在 target - num 则存在
    for (int num : nums) {
      int tmp = map.g etOrDefault(target - num, -1);
      if (tmp != -1) {
        return new int[]{tmp, num};
      }
    }
    return new int[]{};
  }
}

时间复杂度挺高的：O(n^2^) 了，还不如直接遍历，还省内存，我是傻子哈哈~~~

58 - I. 翻转单词顺序

题目：剑指 Offer 58 - I. 翻转单词顺序

剑指 Offer 58 - 1

解题思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Solution {
  public String reverseWords(String s) {
    StringBuilder builder = new StringBuilder();
    s = s.trim(); // 去除首尾空格
    int p = s.length() - 1, q = p;
    while (p >= 0) {
      while (p >= 0 && s.charAt(p) != ' ') {
        p--;
      }
      builder.append(s, p + 1, q + 1).append(" ");
      while (p >= 0 && s.charAt(p) == ' ') {
        p--;
      }
      q = p;
    }
    return builder.toString().trim(); // 去除尾部空格
  }
}

题解思路

看了另一种方法是字符串分割，trim() 去除字符串首尾的空格并且返回修改后的字符串，split(" ") 是按照给定的字符串进行分割，可以使用正则表达式，” （两个空格）” 将会被分割为：["两个","","空格" ]

1
2
3
4
5
6
7
8
9
10
public static String reverseWords(String s) {
  String[] strings = s.trim().split(" ");
  StringBuilder builder = new StringBuilder();
  for (int i = strings.length; i > 0; --i) {
    if (!"".equals(strings[i - 1])) {
      builder.append(strings[i - 1]).append(" ");
    }
  }
  return builder.toString().trim(); // 去除尾部空格
}

✔️Day 14

刷题笔记：《剑指 Offer 第十四天》

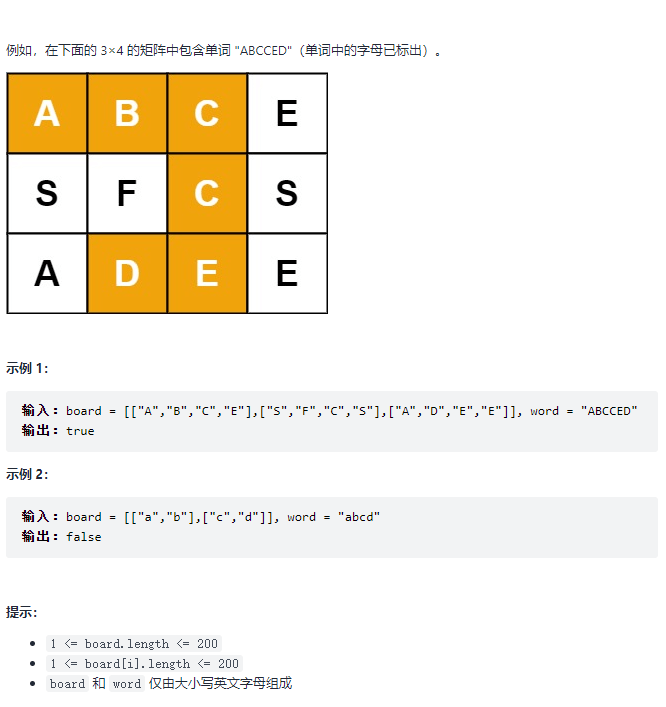
12. 矩阵中的路径

题目：剑指 Offer 12. 矩阵中的路径

剑指 Offer 12

题解思路

本问题是典型的矩阵搜索问题，可使用 深度优先搜索（DFS）+ 剪枝 解决。

  • 深度优先搜索： 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
  • 剪枝： 在搜索中，遇到 这条路不可能和目标字符串匹配成功 的情况（例如：此矩阵元素和目标字符不同、此元素已被访问），则应立即返回，称之为 可行性剪枝 。

图解

DFS 解析：

  • 递归参数： 当前元素在矩阵 board 中的行列索引 i 和 j ，当前目标字符在 word 中的索引 k ；
  • 终止条件：
    1. 返回 false ：（1）行或列越界 或 （2）当前矩阵元素与目标字符不同 或 （3）当前矩阵元素已经访问过了（（3）可以合并至（2））；
    2. 返回 true ：k == words.length() - 1，即字符串 word 已全部匹配；
  • 地推工作：
    1. 标记当前矩阵元素：将 board[i][j] 修改为 空字符 ‘\0’ ，代表此元素已经访问过，防止后续搜索时重复访问；
    2. 搜索下一单元格：朝当前元素的 上、下、左、右 四个方向开启下层递归，使用 || 连接（代表只需要找到一条可行路径就直接返回，不再做后续 DFS），并记录结果至 res；
    3. 还原当前矩阵元素：将 board[i][j] 元素还原至初始值，即 word[k]；
  • 返回值： 返回布尔值 res，代表是否索搜到目标字符串；

题解代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class Solution {
  public boolean exist(char[][] board, String word) {
    char[] words = word.toCharArray();
    for (int i = 0; i < board.length; ++i) {
      for (int j = 0; j < board[0].length; ++j) {
        if (dfs(board, words, i, j, 0)) {
          return true;
        }
      }
    }
    return false;
  }
  public boolean dfs(char[][] board, char[] words, int i, int j, int k) {
    // 越界或不是要搜寻的字符返回 false
    if (i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != words[k]) {
      return false;
    }
    if (k == words.length - 1) {
      return true;
    }
    board[i][j] = '\0'; // 标记代表来过了
    boolean res = dfs(board, words, i + 1, j, k + 1) || dfs(board, words, i - 1, j, k + 1) ||
      dfs(board, words, i, j + 1, k + 1) || dfs(board, words, i, j - 1, k + 1);
    board[i][j] = words[k]; // 复原
    return res;
  }
}

13. 机器人的运动范围

题目：剑指 Offer 13. 机器人的运动范围

剑指 Offer 13

解题思路（dfs）

根据题解写了个最基本的 dfs，dfs 也被称作为 暴力算法，本质上就是枚举，可以解决没有办法确定枚举层数的问题；枚举 + 递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class Solution {
  private int m, n, k;
  private boolean[][] visited;
  public int movingCount(int m, int n, int k) {
    this.m = m;
    this.n = n;
    this.k = k;
    this.visited = new boolean[m][n];
    return dfs(0, 0);
  }
  public int dfs(int i, int j) {
    if (i < 0 || i >= m || j < 0 || j >= n || visited[i][j]) { // 越界
      return 0;
    }
    visited[i][j] = true;
    if (sums(i) + sums(j) > k) { // 数位之和大于 k
      return 0;
    }
    return 1 + (dfs(i + 1, j) + dfs(i - 1, j)
                + dfs(i, j + 1) + dfs(i, j - 1));
  }
  public int sums(int num) {
    int tmp = 0;
    while (num != 0) {
      tmp += num % 10;
      num /= 10;
    }
    return tmp;
  }
}

解题代码（dfs、优化）

然后看到评论区有大佬贴出来的代码，才发现这题的数据范围下标被限制到了 1<= n, m <= 100，也就是说索引值是在 0~99 之间的；所以可以省去 sums 这个函数的调用这一部分，然后又因为是从起点 (0, 0) 出发的，所以只需要向右下两个方向进行搜索即可；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Solution2 {
  private int m, n, k;
  private boolean[][] visited;

  public int movingCount(int m, int n, int k) {
    this.m = m;
    this.n = n;
    this.k = k;
    this.visited = new boolean[m][n];
    return dfs(0, 0);
  }

  public int dfs(int i, int j) {
    if (i >= m || j >= n || visited[i][j]) { // 只向右下搜索，左上不会出现越界问题
      return 0;
    }
    visited[i][j] = true;
    if (i / 10 + i % 10 + j / 10 + j % 10 > k) { // 数位之和大于 k
      return 0;
    }
    return 1 + dfs(i + 1, j) + dfs(i, j + 1);
  }
}

题解思路（bfs）

dfs 是深度优先搜索，一条路走到黑，bfs 是广度优先搜索，有种以 ”平推“ 的方式向前搜索；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public int movingCount(int m, int n, int k) {
  if (k == 0) {
    return 1;
  }
  Queue<int[]> queue = new LinkedList<>();
  boolean[][] visited = new boolean[m][n];
  visited[0][0] = true;
  int res = 1;
  queue.offer(new int[]{0, 0});
  while (!queue.isEmpty()) {
    int[] cell = queue.poll(); // x, y坐标
    int x = cell[0], y = cell[1];
    for (int i = 0; i < 2; ++i) {
      int tx = i + x;
      int ty = y + 1 - i;
      if (tx >= m || ty >= n || visited[tx][ty] || tx / 10 + tx % 10 + ty / 10 + ty % 10 > k) {
        continue;
      }
      queue.offer(new int[]{tx, ty});
      visited[tx][ty] = true;
      res++;
    }
  }
  return res;
}

✔️Day 15

刷题笔记：《剑指 Offer 第十五天》

34. 二叉树中和为某一值的路径

题目：剑指 Offer 34. 二叉树中和为某一值的路径

剑指 Offer 34

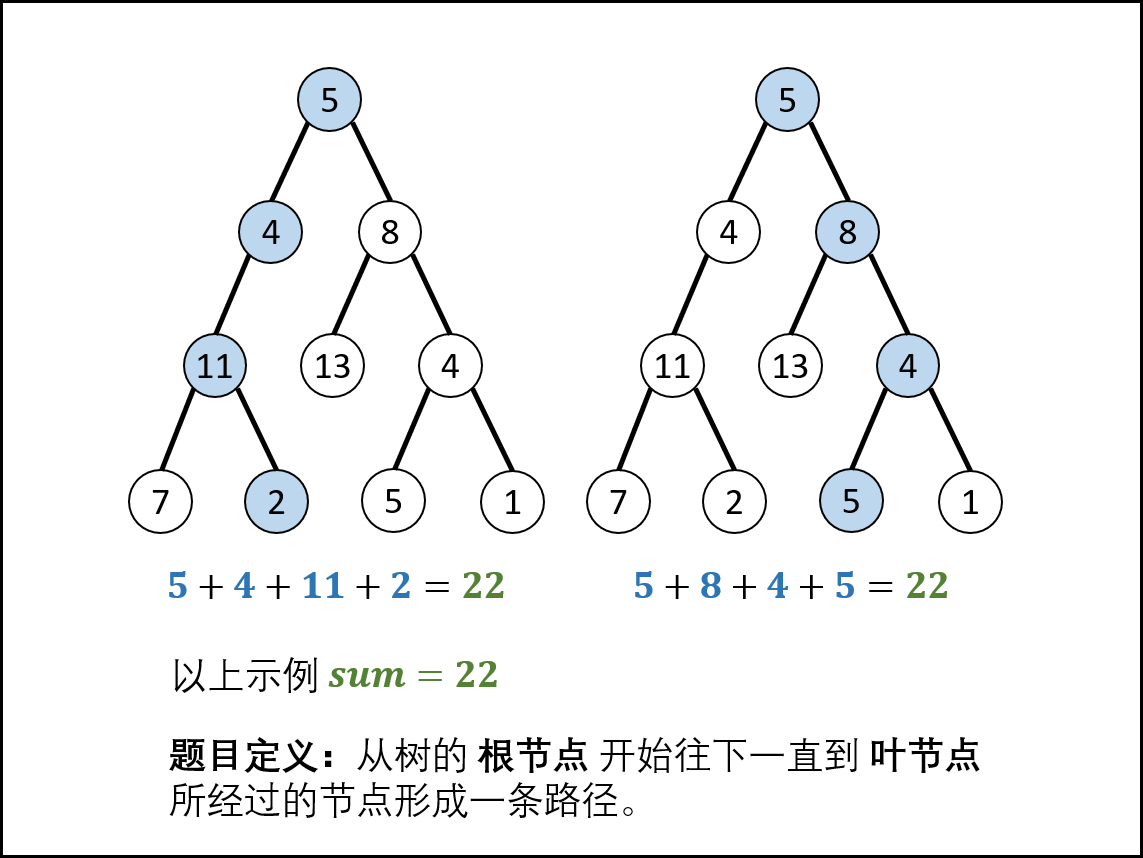
题解思路

本问题是典型的二叉树方案搜索问题，使用回溯法解决，其包含 先序遍历 + 路径记录 两部分

  • 先序遍历： 按照 “根、左、右” 的顺序，遍历树的所有节点
  • 路径记录： 在先序遍历中，记录从根节点到当前节点的路径。当路径为：（1）根节点到叶节点形成的路径 且（2）各节点值的和等于目标值 sum 时，将此路径加入结果列表

图解

算法流程

  • 递推参数： 当前节点 root ，当前目标值 tar 。
  • 终止条件： 若节点 root 为空，则直接返回。
  • 递推工作：
    1. 路径更新： 将当前节点值 root.val 加入路径 path ；
    2. 目标值更新： tar = tar - root.val（即目标值 tar 从 sum 减至 0 ）；
    3. 路径记录： 当 ① root 为叶节点 且 ② 路径和等于目标值 ，则将此路径 path 加入 res；
    4. 先序遍历： 递归左 / 右子节点；
    5. 路径恢复： 向上回溯前，需要将当前节点从路径 path 中删除，即执行 path.pop() ；

复杂度分析

  • 时间复杂度 O(N)： N 为二叉树的节点数，先序遍历需要遍历所有节点。
  • 空间复杂度 O(N)： 最差情况下，即树退化为链表时，path 存储所有树节点，使用 O(N) 额外空间。

题解代码

值得注意的是，记录路径时若直接执行 res.append(path) ，则是将 path 对象加入了 res ；后续 path 改变时， res 中的 path 对象也会随之改变

正确做法：res.append(list(path)) ，相当于复制了一个 path 并加入到 res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Solution {
  LinkedList<List<Integer>> res = new LinkedList<>();
  LinkedList<Integer> path = new LinkedList<>();
  public List<List<Integer>> pathSum(TreeNode root, int target) {
    recur(root, target);
    return res;
  }
  public void recur(TreeNode root, int target) {
    if (root == null) {
      return;
    }
    path.add(root.val);
    target -= root.val;
    if (target == 0 && root.left == null && root.right == null) { // 注意必须是叶子节点
      res.add(new LinkedList<>(path)); // 注意要新 new 一个 LinkedList，否则 path 发生变化时 res 也会跟着变化
    }
    recur(root.left, target);
    recur(root.right, target);
    path.removeLast();
  }
}

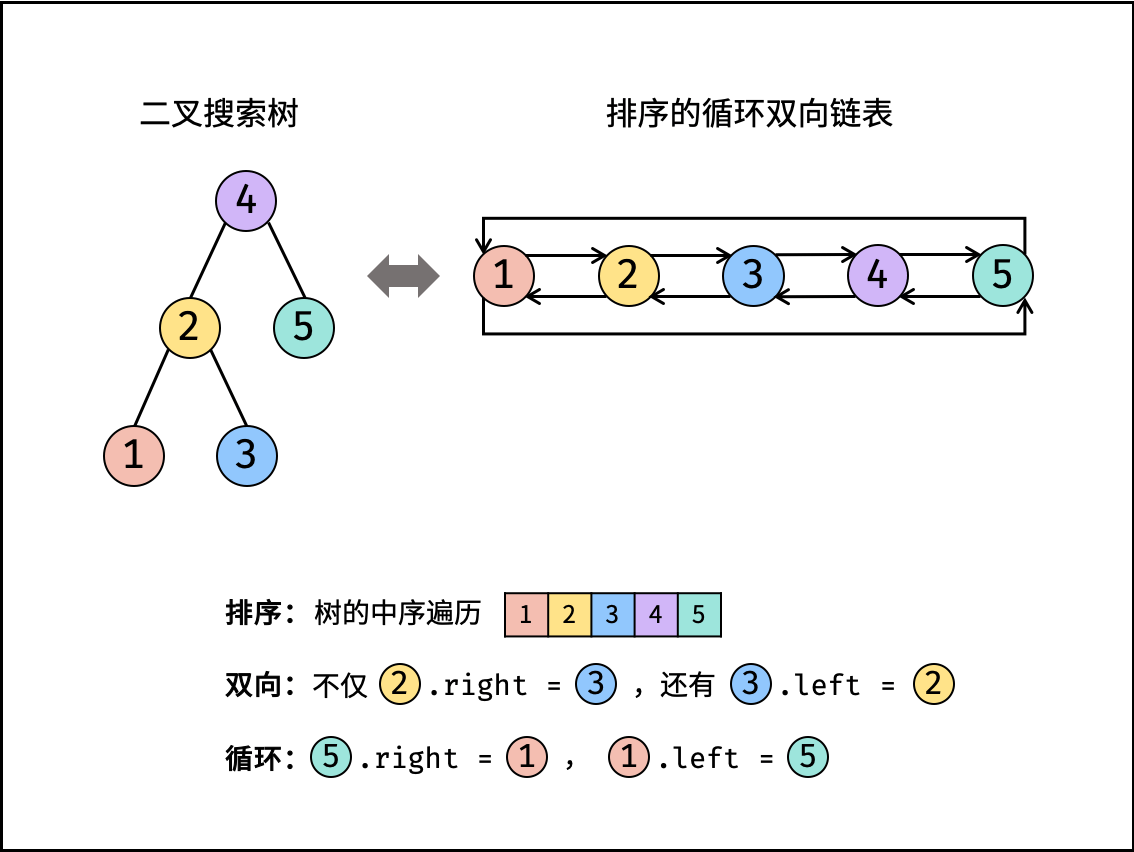
36. 二叉搜索树与双向链表

题目：剑指 Offer 36. 二叉搜索树与双向链表

二叉搜索树：中序遍历是递增序列的数

（一个节点的左子树的所有节点的值比它小，右子树的所有节点的值比它大）

剑指 Offer 36

解题思路

想到中序遍历了，然后第一时间想用栈去存储它，但是想不到怎么从一开始获取栈顶栈顶的元素（head、tail 节点），最后干脆使用 ArrayList 去存储它了；

借个 K 神的图：

图解

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public class Solution {
  private ArrayList<Node> list = new ArrayList<>();
  public Node treeToDoublyList(Node root) {
    if (root == null) { // 特例：[]
      return null;
    }
    if (root.left == null && root.right == null) { // 特例：[1]
      root.left = root;
      root.right = root;
      return root;
    }
    recur(root);

    Node head = list.get(0), tail = list.get(list.size() - 1); // head 头节点 tail 尾节点
    for (int i = 0; i < list.size() - 1; ++i) {
      list.get(i).right = list.get(i + 1);
      list.get(i + 1).left = list.get(i);
    }
    head.left = tail;
    tail.right = head;
    return head;
  }
  public void recur(Node root) { // 中序遍历
    if (root == null) {
      return;
    }
    if (root.left != null) {
      recur(root.left);
    }
    list.add(root);
    if (root.right != null) {
      recur(root.right);
    }
  }
}

54. 二叉搜索树的第k大节点

题目：剑指 Offer 54. 二叉搜索树的第k大节点

剑指 Offer 54

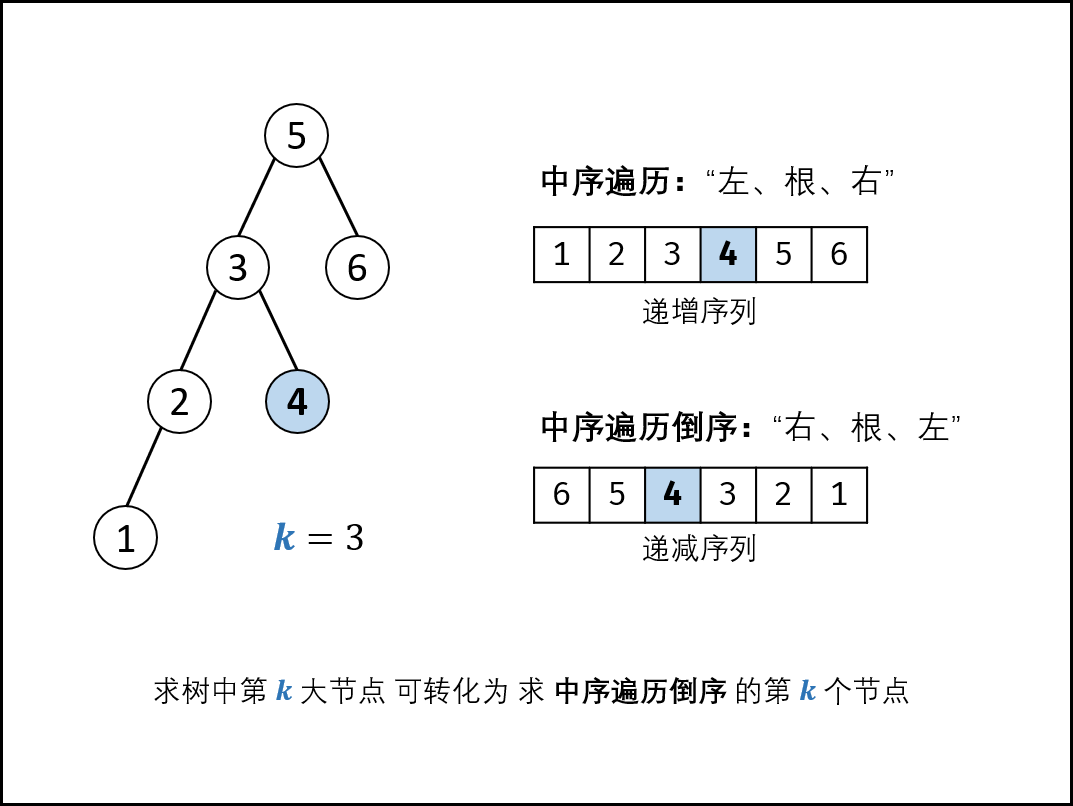
题解思路

二叉搜索树的的中序遍历是递增序列，需要找第 k 大的节点，如果是降序序列会容易一点；中序遍历的过程是：左 中 右，而先 右 中 左 就能满足降序序列，所以将遍历条件稍微修改一下就可以了；

图解

题解代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class Solution {
    private int res, k;
    public int kthLargest(TreeNode root, int k) {
        this.k = k;
        dfs(root);
        return res;
    }
    public void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        dfs(root.right);
        if (k == 0) {
            return;
        }
        k--;
        if (k == 0) {
            res = root.val;
        }
        dfs(root.left);
    }
}

✔️Day 16

刷题笔记：《剑指 Offer 第十六天》

45. 把数组排成最小的数

题目：剑指 Offer 45. 把数组排成最小的数

剑指 Offer 45

解题思路

首先确定一件事就是，不管怎么排序，最后得到的数字的位数都是一样的（特例：前导 0，所以要进行特判）所以每次从数组中找到，高位最小值即可（相同值比较次高位）

例如：

  • 11、10：先选 10
  • 10、1：先选 10

写了两个小时，我承认我是废物了，呜呜，好的看题解去了，写不出来；垃圾代码就不贴出来了

题解思路

大佬不愧是大佬，思路清晰欸，人家直接追根溯源，假设两个数 x 和 y，若拼接后的数字 x + y > y + x，则 x 在本题逻辑上大于 y；

题解代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Solution {
  public String minNumber(int[] nums) {
    StringBuilder builder = new StringBuilder();
    int tmp;
    for (int i = 0; i < nums.length - 1; ++i) {
      for (int j = 0; j < nums.length - 1 - i; ++j) {
        if (compare(nums[j], nums[j + 1]) > 0) {
          tmp = nums[j];
          nums[j] = nums[j + 1];
          nums[j + 1] = tmp;
        }
      }
    }
    for (int num : nums) {
      builder.append(num);
    }
    return builder.toString();
  }
  public int compare(int num1, int num2) {
    return ("" + num1 + num2)
      .compareTo("" + num2 + num1);
  }
}

题解代码（优化）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class Solution {
  public String minNumber(int[] nums) {   
    String[] strs = new String[nums.length];
    for(int i = 0; i < nums.length; i++)
      strs[i] = String.valueOf(nums[i]);
    quickSort(strs, 0, strs.length - 1);
    StringBuilder res = new StringBuilder();
    for(String s : strs)
      res.append(s);
    return res.toString();
  }
  void quickSort(String[] strs, int l, int r) {
    if(l >= r) return;
    int i = l, j = r;
    String tmp = strs[i];
    while(i < j) {
      while((strs[j] + strs[l]).compareTo(strs[l] + strs[j]) >= 0 && i < j) j--;
      while((strs[i] + strs[l]).compareTo(strs[l] + strs[i]) <= 0 && i < j) i++;
      tmp = strs[i];
      strs[i] = strs[j];
      strs[j] = tmp;
    }
    strs[i] = strs[l];
    strs[l] = tmp;
    quickSort(strs, l, i - 1);
    quickSort(strs, i + 1, r);
  }
}

61. 扑克牌中的顺子

题目：剑指 Offer 61. 扑克牌中的顺子

剑指 Offer 61

解题思路

此题有个小坑，需要注意的是从若干副扑克牌中抽取五张牌，并不是一副扑克牌中，所以有可能会出现如下的特例：[0, 0, 0, 0, 0]

俺没有很好的抽象思维能力，根据样例想出来了若没有癞子将数组通过两两迭代（无需排序）最后结果为 4 就可以（等差数列），然后就成功写出来了垃圾代码，居然还通过了 95% 的样例；

之后考虑上癞子卡了一会，提交失败后发现特例：[0, 0, 2, 2, 5]；于是发现了自己没有进行相同非癞子牌的判别，加入特判后成功通过；

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
public boolean isStraight(int[] nums) {
  Arrays.sort(nums);
  int joker = 0;
  for (int i = 0; i < 4; ++i) {
    if (nums[i] == 0) {
      joker++;
    } else if (nums[i] == nums[i + 1]){
      return false;
    }
  }
  return nums[4] - nums[joker] < 5;
}

题解思路

看了下题解，难得自己和大佬代码写了一样了一次，然后还有一种思路是通过 set 去维护牌组，若有相同的直接返回 false，其他操作一样；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public boolean isStraight(int[] nums) {
  Set<Integer> set = new HashSet<>();
  int max = 0, min = 14;
  for (int num: nums) {
    if (num == 0) continue;
    max = Math.max(max, num);
    min = Math.min(min, num);
    if (set.contains(num)) {
      return false;
    }
    set.add(num);
  }
  return max - min < 5;
}

✔️Day 17

刷题笔记：《剑指 Offer 第十七天》

40. 最小的k个数

题目：剑指 Offer 40. 最小的k个数

剑指 Offer 40

解题思路

第一时间想到了冒泡排序，找出 k 大的有序区域返回即可；提交通过后那个用时和内存消耗把自己整笑了，又是写了垃圾代码的一天；

解题通过

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {
  public int[] getLeastNumbers(int[] arr, int k) {
    int tmp;
    for (int i = 0; i < k; ++i) {
      for (int j = arr.length - 1; j > i; --j) {
        if (arr[j] < arr[j - 1]) {
          tmp = arr[j];
          arr[j] = arr[j - 1];
          arr[j - 1] = tmp;
        }
      }
    }
    return Arrays.copyOf(arr, k);
  }
}

41. 数据流中的中位数

题目：剑指 Offer 41. 数据流中的中位数

剑指 Offer 41

思路

第一时间想到的是维护一个有序的动态数组，然后用个“指针”一直指向中间元素，根据数组元素的奇、偶去获取中值，但是想了想这么做好像没法剑指offer了，面试官可能一脚给我踢出来了，所以看了题解去了；

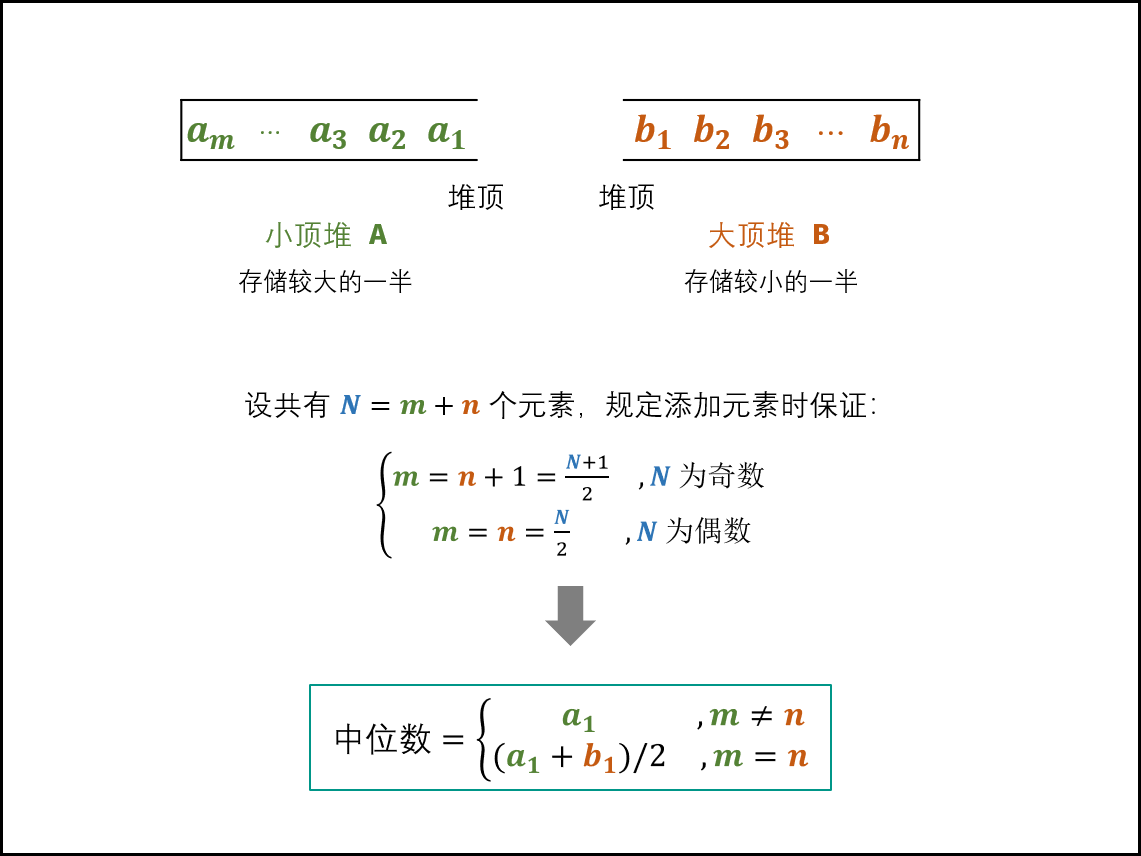
题解思路

借助 堆 进一步优化时间复杂度，建立一个小顶堆 A 和 大顶堆 B，各保存列表的一半元素，且规定：

  • A 保存 较大 的一半，长度为 $\frac{N}{2}$（ N 为偶数）或 $\frac{N + 1}{2}$ （N 为奇数）
  • B 保存 较小 的一半，长度为 $\frac{N}{2}$ （N 为偶数）或 $\frac{N - 1}{2}$ （N 为奇数）

图解

算法流程

设元素总数为 N = m + n，其中 m 和 n 分别为 A 和 B 中的元素个数。

A 小顶堆中存储较大的一半，B 大顶堆中存储较小的一半，这样之后 A 的堆顶的值 >= B的堆顶的值，即 A 中的最小值大于等于 B 中的最大值；

addNum(num) 函数：

  1. 当 m = n（即 N 为偶数）：需向 A 添加一个元素，实现方法：将新元素 num 插入 B，再将 B 堆顶元素插入至 A（确保上面的那个性质）
  2. 当 m != n（即 N 为奇数）：需向 B 添加一个元素。实现方法：将新元素 num 插入至 A ，再将 A 堆顶元素插入至 B ；

findMedian() 函数：

  1. 当 m = n （N 为偶数）：则中位数为（A 的堆顶元素 + B 的堆顶元素）/ 2
  2. 当 m != n （N 为奇数）：则中位数为 A 的堆顶元素；

复杂度分析

  1. 时间复杂度：
    • 查找中位数 O(1)：获取堆顶元素使用 O(1) 时间
    • 添加数字 O(log N)：堆的插入和弹出操作使用 O(log N) 时间
  2. 空间复杂度 O(N)：其中 N 为数据流中的元素数量，小顶堆 A 和大顶堆 B 最多同时保存 N 个元素

题解代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public class MedianFinder {
  public static void main(String[] args) {
    // 默认是小顶堆
    Queue<Integer> A = new PriorityQueue<>();
    // 传入自定义比较器（lambda 表达式）作用同 C
    Queue<Integer> B = new PriorityQueue<>((x, y) -> y - x);
    Queue<Integer> C = new PriorityQueue<>(new Comparator<Integer>() {
      @Override
      public int compare(Integer o1, Integer o2) {
        return o2 - o1;
      }
    });
  private Queue<Integer> A, B;
  /**
   * initialize your data structure here.
   */
  public MedianFinder() {
    // 小顶堆
    A = new PriorityQueue<>();
    // 大顶堆
    B = new PriorityQueue<>((x, y) -> (y - x));
  }
  public void addNum(int num) {
    if (A.size() != B.size()) {
      A.add(num);
      B.add(A.poll());
    } else {
      B.add(num);
      A.add(B.poll());
    }
  }
  public double findMedian() {
    return A.size() != B.size() ? A.peek() : (A.peek() + B.peek()) / 2.0;
  }
}

✔️Day 18

刷题笔记：《剑指 Offer 第十八天》

55 - I. 二叉树的深度

题目：剑指 Offer 55 - I. 二叉树的深度

剑指 Offer 55 - 1

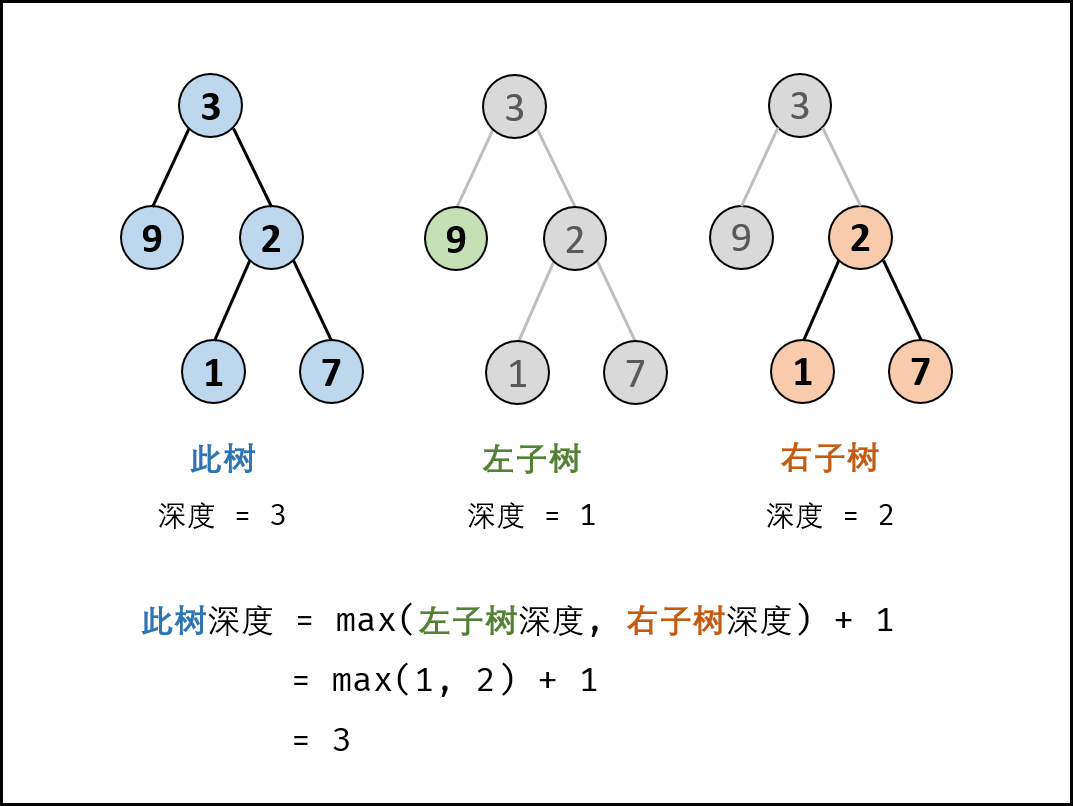
稍微分析之后可以得出规律：对于一个非叶子节点的节点 node，它的深度为 max(deep(node.left), deep(node.right)) + 1，所以可以很轻松写出来递归解法：

图解

复杂度分析

  • 时间复杂度 O(N)：N 为树的节点个数，dfs 计算需要遍历到树的每一个节点；
  • 空间复杂度 O(N)：最差情况下（树退化为链表时（所有非叶子节点都只有一个方向上的子节点）），递归深度可达到 N

解题代码

1
2
3
4
5
6
7
8
public class Solution {
  public int maxDepth(TreeNode root) {
    if (root == null) {
      return 0;
    }
    return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
  }
}

题解思路

二叉树的常见四种遍历方式中，层序遍历（BFS）显然与深度有关，可以在层序遍历的过程中每遍历一层使用计数器统计深度即可；

题解代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution {
  public int maxDepth(TreeNode root) {
    if(root == null) return 0;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    int res = 0;
    while(!queue.isEmpty()) {
      res++;
      for(int i = queue.size(); i > 0;--i) { // 注意队列动态变化，queue.size() 也跟着变化
        TreeNode node = queue.poll(); // 利用队列先进先出的特点
        if(node.left != null) queue.offer(node.left);
        if(node.right != null) queue.offer(node.right);
      }
    }
    return res;
  }
}

55 - II. 平衡二叉树

题目：剑指 Offer 55 - II. 平衡二叉树

剑指 Offer 55 - 2

解题思路

在上一题的基础上对每个非叶子节点进行判断即可；有许多重复性的操作，效率较低；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution {
  public boolean isBalanced(TreeNode root) {
    if (root == null) {
      return true;
    }
    return (Math.abs(dfs(root.left) - dfs(root.right)) <= 1)
      && isBalanced(root.left) && isBalanced(root.right);
  }
  public int dfs(TreeNode root) {
    if (root == null) {
      return 0;
    }
    int left = dfs(root.left);
    int right = dfs(root.right);
    return Math.max(left, right) + 1;
  }
}

题解思路

在原有基础上进行剪枝，当发现已经不是 平衡二叉树 时，提前返回；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
  public boolean isBalanced(TreeNode root) {
    return dfs(root) != -1;
  }
  public int dfs(TreeNode root) {
    if (root == null) {
      return 0;
    }
    int left = dfs(root.left);
    if (left == -1) {
      return -1;
    }
    int right = dfs(root.right);
    if (right == -1) {
      return -1;
    }
    return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
  }
}

✔️Day 19

刷题笔记：《剑指 Offer 第十九天》

64. 求1+2+…+n

题目：剑指 Offer 64. 求1+2+…+n

剑指 Offer 64

题解思路

我想打表，他说我代码太长了，哭，他把我能用的符号都给 ban 了，我实在是想不到思路了，看了评论区，秀的我天花乱坠；

有面试官看到了就请你出去类型的题解：

1
2
3
int sumNums(int n) {   
  return int(Math.pow(n, 2) + n) >> 1;
}

也有我不知道怎么翻译到 Java 类型的 C++ 题解：

1
2
3
4
int sumNums(int n) {   
  bool arr[n][n+1];
  return sizeof(arr) >> 1;
}

有C语言内联汇编的（汇编都出来了，牛的）题解：

1
2
3
4
5
6
7
8
9
10
11
int sumNums(int n) {   
  int res;
  __asm(
    "movl %%edi, %%eax\n"
    "incl %%edi\n"
    "imull %%edi\n"
    "shrl $1, %%eax\n"
    :"=a"(res)
  );
  return res;
}

还有自己实现乘法逻辑的题解：

1
2
3
4
5
6
7
8
9
int sumNums(int n) {   
  return multiply(n,n+1) >> 1; // 等价于 n * (n + 1) / 2
}
int multiply(int A, int B) {
  int res = B;
  // A == 1 时，短路，不执行 && 后面的代码
  (A != 1) && (res = ((( -(A & 1)) & B) + multiply(A >> 1, B << 1)));        
  return res;
}

还有我想到了递归却想不到究竟该如何求解类型的题解：

图解

1
2
3
4
5
6
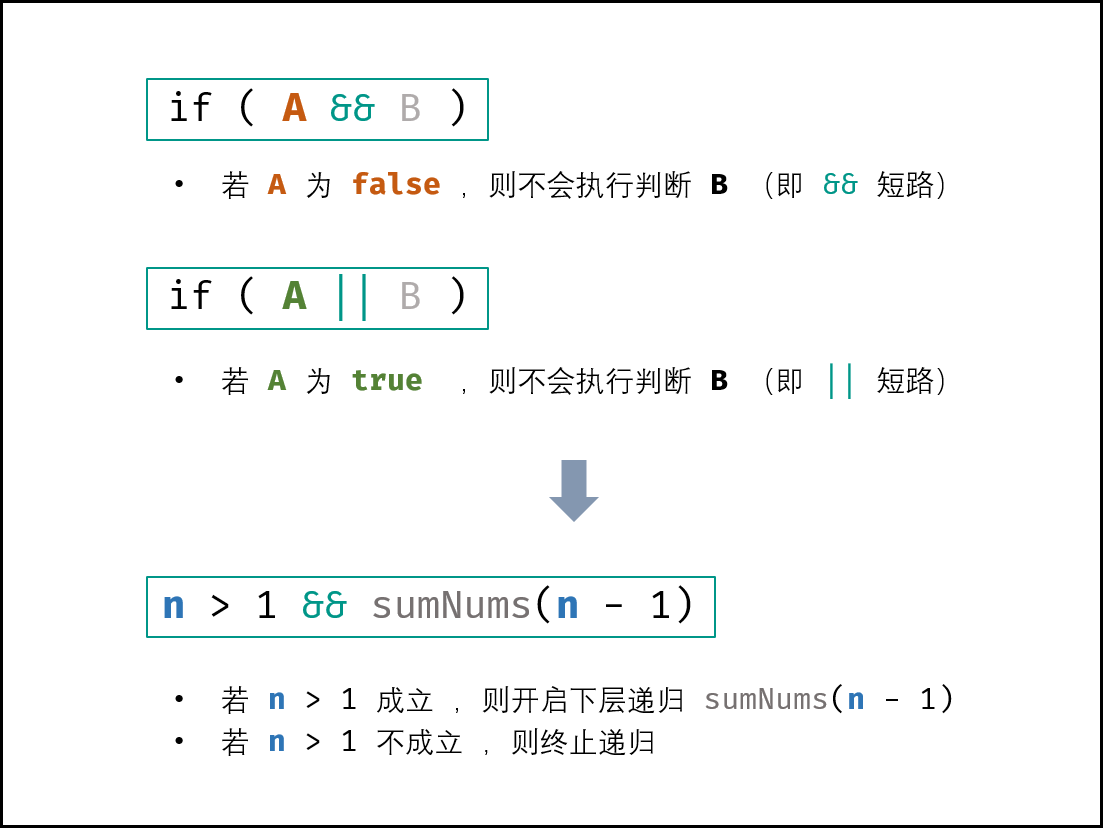
int sumNums(int n) {   
  int sum = n;
  // 巧妙利用 "短路" 特性，当 n 大于 0 时 就继续递归，否则停止递归 return 前面的累加值
  boolean flag = n > 0 && sum += sumNums(n - 1) > 0;
  return sum;
}

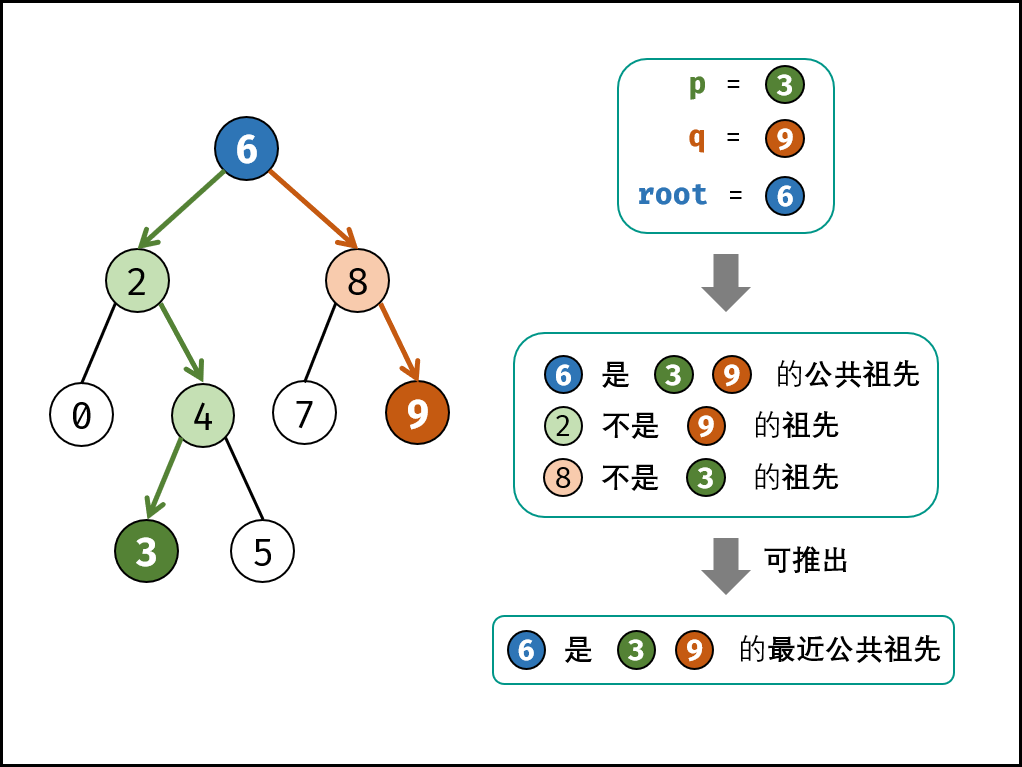
68 - I. 二叉搜索树的最近公共祖先

题目：剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

剑指 Offer 68 - 1

解题思路

二叉搜索树 有如下的性质： 对于一个非叶子节点，它的左节点的值比它小，它的右节点的值比它大。

给定的条件还有所有的节点值都是 唯一且存在的 ，所以可以根据节点 p、q 的值去判断节点 p、q 和 根节点 root 的位置关系；

图解

  1. p.val < root.val && q.val < root.val：p、q 在 root 节点的左子树上，遍历 root.left ；
  2. p.val > root.val && q.val > root.val：p、q 在 root 节点的右子树上，遍历 root.right ；
  3. p.val == root.val || q.val == root.val：p(或 q) 是 q(或 p) 的父节点，直接返回 root 即可；
  4. p.val < root.val && q.val > root.val || p.val > root.val && q.val < root.val：p、q 在 root 节点的两侧，直接返回 root 即可；

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
  public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    // p、q 在根节点两侧，公共祖先一定是 root; 或者 p(q) 是 q(p) 的父节点
    if (p.val > root.val && q.val < root.val || p.val < root.val && q.val > root.val || p.val == root.val || q.val == root.val) {
      return root;
    }
    // p、q 在根节点左侧
    if (p.val < root.val && q.val < root.val) {
      return lowestCommonAncestor(root.left, p, q);
    }
    // p、q 在根节点右侧
    return lowestCommonAncestor(root.right, p, q);
  }
}

解题代码—优化？

emmmmm，优化完提交了一下才发现好像是负面优化：5ms 42.5MB -> 6ms 42.4MB，但是代码逻辑上来说更清晰了，负面优化的原因应该是： 递归终止条件没在开头

1
2
3
4
5
6
7
8
9
10
11
12
public class Solution {
  public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (p.val < root.val && q.val < root.val) { // p、q 同侧，左子树
      return lowestCommonAncestor(root.left, p, q);
    }
    if (p.val > root.val && q.val > root.val) { // p、q 同侧，右子树
      return lowestCommonAncestor(root.right, p, q);
    }
    // p、q 在根节点两侧，公共祖先一定是 root; 或者 p(q) 是 q(p) 的父节点
    return root;
  }
}

解题代码—再优化

如果可以保证 p、q 的大小一定（例如：p < q），那么可以省去许多判断；5ms 42.5MB

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Solution {
  public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (p.val > q.val) {
      TreeNode tmp = p;
      p = q;
      q = tmp;
    }
    return recur(root, p, q);
  }
  public TreeNode recur(TreeNode root, TreeNode p, TreeNode q) {
    if (q.val < root.val) { // p < q < root, p、q 同侧, 遍历左子树
      return recur(root.left, p, q);
    }
    if (p.val > root.val) { // root < p < q, p、q 同侧, 遍历右子树
      return recur(root.right, p, q);
    }
    // p、q 在根节点两侧，公共祖先一定是 root; 或者 p(q) 是 q(p) 的父节点
    return root;
  }
}

5ms 42.4 MB

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class Solution {
  public static TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (p.val > q.val) {
      TreeNode tmp = p;
      p = q;
      q = tmp;
    }
    return recur(root, p, q);
  }
  public static TreeNode recur(TreeNode root, TreeNode p, TreeNode q) {
    // p、q 在根节点两侧，公共祖先一定是 root; 或者 p(q) 是 q(p) 的父节点
    if (p.val < root.val && q.val > root.val || p.val == root.val || q.val == root.val) {
      return root;
    }
    // p、q 在根节点左侧
    if (q.val < root.val) {
      return recur(root.left, p, q);
    }
    // p、q 在根节点右侧
    return recur(root.right, p, q);
  }
}
题解代码（非递归）

5ms 42.2 MB

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution {
  public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if(p.val > q.val) { // 保证 p.val < q.val
      TreeNode tmp = p;
      p = q;
      q = tmp;
    }
    while(root != null) {
      if(root.val < p.val) // p,q 都在 root 的右子树中
        root = root.right; // 遍历至右子节点
      else if(root.val > q.val) // p,q 都在 root 的左子树中
        root = root.left; // 遍历至左子节点
      else break;
    }
    return root;
  }
}

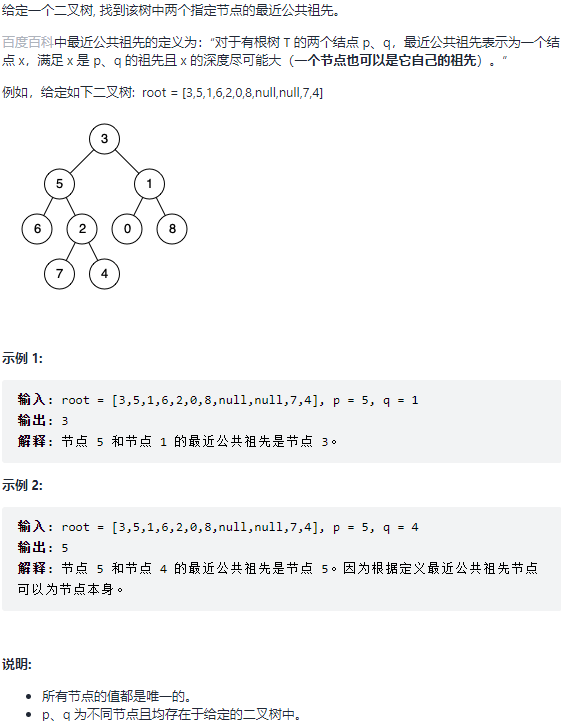
68 - II. 二叉树的最近公共祖先

题目：剑指 Offer 68 - II. 二叉树的最近公共祖先

剑指 Offer 68 - 2

解题思路

与上一题不同的是这是一颗普通的二叉树，也就是没有了： 对于一个非叶子节点，它的左节点的值比它小，它的右节点的值比它大。 这个性质了；

LeetCode
刷题

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！